
分析 (1)在已知数列递推式中取n=1,得a3-a1=2,以n-1替换n,与原递推式联立可得2an=an+1+an-1,进一步说明数列{an}是首项为a,公差为1的等差数列.则通项公式可求;
(2)求出等差数列的前n项和,配方后结合Sn≥S10对一切n∈N*都成立,得到关于a的不等式,求解不等式得到实数a的取值范围.
解答 解:(1)由Sn=$\frac{n({a}_{n}+{a}_{3}-2)}{2}$,①令n=1,得2a1=a1+a3-2,则a3-a1=2,
又${S}_{n-1}=\frac{(n-1)({a}_{n-1}+{a}_{3}-2)}{2}$,②
①-②得:${a}_{n}=\frac{n({a}_{n}+{a}_{3}-2)}{2}-\frac{(n-1)({a}_{n-1}+{a}_{3}-2)}{2}$,
得(n-2)an=(n-1)an-1-a3+2,③
则(n-1)an+1=nan-a3+2,④
④-③得:(n-1)an+1-(n-2)an=nan-(n-1)an-1,
∵n≥2,∴有2an=an+1+an-1,⑤
由a3-a1=2和⑤知:数列{an}是首项为a,公差为1的等差数列.
∴an=a+(n-1)•1=n+a-1;
(2)${S}_{n}=\frac{n(a+n+a-1)}{2}=\frac{1}{2}[(n-\frac{1-2a}{2})^{2}-\frac{(1-2a)^{2}}{4}]$.
∵Sn≥S10对一切n∈N*都成立,∴$9.5≤\frac{1-2a}{2}≤10.5$,
解得a∈[-10,-9].
点评 本题考查数列递推式,考查了等差关系的确定,考查等差数列的前n项和,训练了恒成立问题的求解方法,是中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | (-∞,1]∪[3,+∞) | C. | [3,+∞) | D. | (0,1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
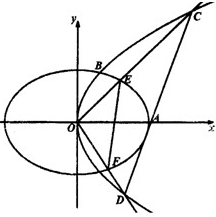 如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的长半轴相等,设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$.
如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的长半轴相等,设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一、二象限 | B. | 第二、三象限 | C. | 第三、四象限 | D. | 第一、四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是正三角形,B1C1∥BC,B1C1=$\frac{1}{2}$BC.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是正三角形,B1C1∥BC,B1C1=$\frac{1}{2}$BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com