
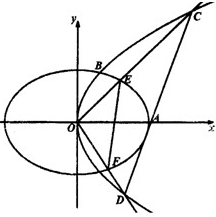
 如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的长半轴相等,设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$.
如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的长半轴相等,设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$.分析 (1)p=2,得椭圆的长半轴a=2,由△OAB的面积为$\frac{1}{2}×2×{y}_{B}$=$\frac{{2\sqrt{6}}}{3}$,知B的坐标.代入抛物线能求出椭圆C2方程.
(2)①设直线l的方程为:x=my+2,与抛物线方程联立,得y2-4my-8=0,利用韦达定理和向量的数量积导出∠COD>90°,由此能证明结论;
②$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\frac{1}{2}|OC|•|OD|sin∠COD}{\frac{1}{2}|OE||OF|sin∠EOF}$=$\frac{|{y}_{1}|}{|{y}_{E}|}$•$\frac{|{y}_{2}|}{|{y}_{F}|}$,求出直线OC的方程,与椭圆方程联立,利用3S2=13S1,由此能推导出存在直线l使得3S2=13S1.
解答 解:(1)抛物线C1:y2=4x中,p=2,得椭圆的长半轴a=2,
∵△OAB的面积为$\frac{1}{2}×2×{y}_{B}$=$\frac{{2\sqrt{6}}}{3}$,
∴yB=$\frac{{2\sqrt{6}}}{3}$.
代入抛物线求得B($\frac{2}{3}$,$\frac{{2\sqrt{6}}}{3}$),
∴椭圆C2方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)①设直线l的方程为:x=my+2,
由$\left\{\begin{array}{l}{x=my+2}\\{{y}^{2}=4x}\end{array}\right.$,得y2-4my-8=0,
设C(x1,y1),D(x2,y2),
∴y1+y2=4m,y1y2=-8,
∴x1x2=4,
∴x1x2+y1y2=-4<0,
∴∠COD>90°,
∴∠COD恒为钝角.
②$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\frac{1}{2}|OC|•|OD|sin∠COD}{\frac{1}{2}|OE||OF|sin∠EOF}$=$\frac{|{y}_{1}|}{|{y}_{E}|}$•$\frac{|{y}_{2}|}{|{y}_{F}|}$,
直线OC的斜率为$\frac{{y}_{1}}{{x}_{1}}$=$\frac{4}{{y}_{1}}$,
∴直线OC的方程为x=$\frac{{y}_{1}y}{4}$.
与椭圆方程联立,得yE2=$\frac{64×3}{3{{y}_{1}}^{2}+64}$,yF2=$\frac{64×3}{3{{y}_{2}}^{2}+64}$,
∴yE2•yF2=$\frac{64×{3}^{2}}{121+48m}$,
∴($\frac{{S}_{1}}{{S}_{2}}$)2=$\frac{121+48{m}^{2}}{{3}^{2}}$=$\frac{1{3}^{2}}{{3}^{2}}$,
∴m=±1,
∴直线l的方程为:x=±y+2.
点评 本题考查椭圆方程的求法,探索满足条件的直线方程是否存在.综合性强,难度大,对数学思维的要求较高.解题时要认真审题,仔细解答,注意等价转化思想的合理合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x+1 | B. | $f(x)=-\frac{1}{x}$ | C. | f(x)=x2 | D. | f(x)=x3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com