
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的极值点;
的极值点;
(Ⅱ)若直线![]() 过点
过点![]() ,并且与曲线
,并且与曲线![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(Ⅲ)设函数![]() ,其中
,其中![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值.(其中
上的最小值.(其中![]() 为自然对数的底数)
为自然对数的底数)
【答案】(Ⅰ)![]() 是函数
是函数![]() 的极小值点,极大值点不存在. (Ⅱ)
的极小值点,极大值点不存在. (Ⅱ)![]()
(Ⅲ) 当![]() 时,
时,![]() 的最小值为0;当1<a<2时,
的最小值为0;当1<a<2时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]()
【解析】
试题(Ⅰ)![]() >0 ………1分
>0 ………1分
而![]() >0
>0![]() lnx+1>0
lnx+1>0![]()
![]() >
>![]() <0
<0![]()
![]() <0
<0![]() 0<
0<![]() <
<![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增 . …………3分
上单调递增 . …………3分
所以![]() 是函数
是函数![]() 的极小值点,极大值点不存在. …………………4分
的极小值点,极大值点不存在. …………………4分
(Ⅱ)设切点坐标为![]() ,则
,则![]() 切线的斜率为
切线的斜率为![]()
所以切线![]() 的方程为
的方程为![]() …………5分
…………5分
又切线![]() 过点
过点![]() ,所以有
,所以有![]()
解得![]() 所以直线
所以直线![]() 的方程为
的方程为![]() ………6分
………6分
(Ⅲ)![]() ,则
,则![]()
![]() <0
<0![]() <0
<0![]() 0<
0<![]() <
<![]() >0
>0![]() >
>![]() 所以
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增. ………………8分
上单调递增. ………………8分
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上的最小值为
上的最小值为![]() ……9分
……9分
当1<![]() <e,即1<a<2时,
<e,即1<a<2时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() 在
在![]() 上的最小值为
上的最小值为![]() ………11分
………11分
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 上的最小值为
上的最小值为![]() ……12分
……12分
综上,当![]() 时,
时,![]() 的最小值为0;当1<a<2时,
的最小值为0;当1<a<2时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ………14分
………14分


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足2an=2+Sn.
(1)求证:数列{an}是等比数列;
(2)设bn=log2a2n+1,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
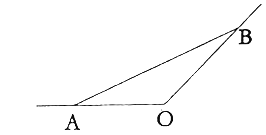
【题目】如图所示,某城市有一条从正西方AO通过市中心O后向东北OB的公路,现要修一条地铁L,在OA,OB上各设一站A,B,地铁在AB部分为直线段,现要求市中心O与AB的距离为![]() ,设地铁在AB部分的总长度为
,设地铁在AB部分的总长度为![]() .
.
![]() 按下列要求建立关系式:
按下列要求建立关系式:
![]() 设
设![]() ,将y表示成
,将y表示成![]() 的函数;
的函数;
![]() 设
设![]() ,
,![]() 用m,n表示y.
用m,n表示y.
![]() 把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为预防![]() 病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于
病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于![]() %,则认为测试没有通过),公司选定
%,则认为测试没有通过),公司选定![]() 个流感样本分成三组,测试结果如下表:
个流感样本分成三组,测试结果如下表:
|
|
| |
疫苗有效 |
|
|
|
疫苗无效 |
|
|
|
已知在全体样本中随机抽取![]() 个,抽到
个,抽到![]() 组疫苗有效的概率是
组疫苗有效的概率是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)现用分层抽样的方法在全体样本中抽取![]() 个测试结果,问应在
个测试结果,问应在![]() 组抽取多少个?
组抽取多少个?
(Ⅲ)已知![]() ,
,![]() ,求不能通过测试的概率.
,求不能通过测试的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com