
 某校为了解2015年高一年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如表的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
某校为了解2015年高一年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如表的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.| 类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
| 册数(本) | 128 | m | 80 | 48 |
分析 (1)首先根据科普类所占的百分比和册数求得总册数,然后相减即可求得m的值;用教辅类书籍除以总册数乘以周角即可求得其圆心角的度数;
(2)用该年级的总人数乘以教辅类的学生所占比例,即可求出该年级共借阅教辅类书籍人数.
解答 解:(1)观察扇形统计图知:科普类有128册,占40%,
∴借阅总册数为128÷40%=320本,∴m=320-128-80-48=64;…..(2分)
教辅类的圆心角为:360°×$\frac{64}{320}$=72°; …..(3分)
(2)设高一年级500名学生借阅教辅类书籍x本,
根据题意得:$\frac{x}{64}=\frac{500}{40}$,解得:x=800,
∴高一年级500名学生中估计共借阅教辅类书籍约800本. …(7分)
点评 此题主要考查了统计表与扇形图的综合应用,读懂统计图,从不同的统计图(表)中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.


科目:高中数学 来源: 题型:选择题
| A. | x2=2y | B. | x2=4y | C. | x2=8y | D. | x2=16y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
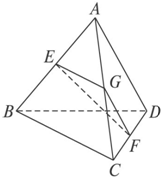 如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.
如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 35 | C. | 32 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{16}{7}$) | B. | (-∞,2) | C. | ($\frac{16}{7}$,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com