练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．设集合A={x|-1＜x＜4}，B={x|-5＜x＜$\frac{3}{2}$}，C={x|1-2a＜x＜2a}．若C⊆（A∩B），求实数a的取值范围．

    分析 先求出A∩B，再根据条件C⊆（A∩B），建立条件关系即可求实数a的取值范围．

    解答 解：当C=ϕ时，1-2a≥2a，$a≤\frac{1}{4}$，
    当C≠ϕ，$A∩B=\{x|-1＜x＜\frac{3}{2}\}$，且C⊆（A∩B）．
    ∴$\left\{\begin{array}{l}1-2a＜2a\\ 2a≤\frac{3}{2}\\ 1-2a≥-1\end{array}\right.$，解得：$\frac{1}{4}＜a≤\frac{3}{4}$．
    综上实数a的取值范围是$（-∞，\frac{3}{4}]$．

    点评 本题主要考查集合的基本运算，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．某校为了解2015年高一年级学生课外书籍借阅情况，从中随机抽取了40名学生课外书籍借阅情况，将统计结果列出如表的表格，并绘制成如图所示的扇形统计图，其中科普类册数占这40名学生借阅总册数的40%．
    （1）求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角a的度数；
    （2）该校2015年高一年级有500名学生，请你估计该年级学生共借阅教辅类书籍约多少本？
    类别科普类教辅类文艺类其他
    册数（本）128m8048

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

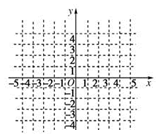    17．已知函数f（x）=x2-2|x|．
    （1）去绝对值，把函数f（x）写成分段函数的形式，并作出其图象；
    （2）求函数f（x）的单调区间；
    （3）求函数f（x）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．函数y=$\left\{\begin{array}{l}{|cosx|，x＞1}\\{0，x≤1}\end{array}\right.$，则：f（1）=0；f（$\frac{π}{6}$）=$\frac{\sqrt{3}}{2}$；f（π）=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．设集合A={-1，0，1}，B={a，a2}，则使A∪B=A成立的a的值是-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知A，B是球O的球面上的两点，∠AOB=$\frac{π}{2}$，C为该球球面上的动点，若三棱锥O-ABC体积的最大值为3，则球的体积为24π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，四边形ABCD为矩形，EA⊥平面ABCD，EF∥AB，AB=2AE=2EF=4．
    （1）设G为BC的中点，求证：FG∥平面BDE；
    （2）求证：AF⊥平面FBC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知全集U={x|x≤5}，集合A={x|-3＜x＜4}，B={x|-5≤x≤3}，则（∁UA）∩B=（　　）
    A．{x|-5≤x≤-3}B．{x|4＜x＜5，或x≤-3}C．{x|-5＜x＜-3}D．{x|-5＜x＜5}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

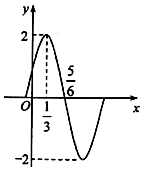    16．函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的图象（部分）如图．
    （1）求f（x）解析式
    （2）若$α∈（{0，\frac{π}{3}}），且f（{\frac{α}{π}}）=\frac{4}{3}$，求cosα．

    查看答案和解析>>

    同步练习册答案