
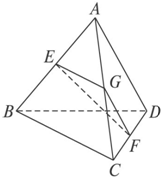
 如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.
如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角. 分析 取AC中点G,连结EG、FG,由已知得EG∥BC,FG∥AD,从而∠EGF是异面直线AD和BC所成的角(或所成角的补角),由此有求出异面直线AD和BC所成的角.
解答 解:取AC中点G,连结EG、FG,
∵E,F分别是AB,CD的中点,∴EG∥BC,FG∥AD,
∴∠EGF是异面直线AD和BC所成的角(或所成角的补角),
设AD=BC=2,EF=$\sqrt{2}$,
∴EG=$\frac{1}{2}BC$=1,FG=$\frac{1}{2}AD$=1,
∴EG2+FG2=EF2,
∴∠EGF=90°,
∴异面直线AD和BC所成的角为90°.
点评 本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|$\frac{1}{2}$<y<1} | B. | {y|0<y$<\frac{1}{2}$} | C. | ∅ | D. | {y|0<y<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校为了解2015年高一年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如表的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
某校为了解2015年高一年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如表的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.| 类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
| 册数(本) | 128 | m | 80 | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com