学校为了解高二年级l203名学生对某项教改试验的意见.打算从中抽取一个容量为40的样本.考虑用系统抽样.则分段的间隔k为30．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

19．学校为了解高二年级l203名学生对某项教改试验的意见，打算从中抽取一个容量为40的样本，考虑用系统抽样，则分段的间隔k为30．

分析由题意知了解1203名学生对学校某项教改试验的意见，打算从中抽取一个容量为40的样本，1203除以40不是整数，先随机的去掉3个人，再除以40，得到每一段有30个人，在抽样过程中每个个体被抽到的概率相等．

解答解：了解1203名学生对学校某项教改试验的意见，
打算从中抽取一个容量为40的样本，
∵1203除以40不是整数，
∴先随机的去掉3个人，再除以40，得到每一段有30个人，
则分段的间隔k为30．
故答案为30．

点评本题考查系统抽样，系统抽样是对于样本中个体比较多，且个体之间没有明显的差距，可以采用系统抽样，在抽样过程中，若出现总体数不能被样本容量整除，则要剔除几个个体．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

9．在△ABC中，∠BAC=120°，AB=2，AC=1，P是BC边上的一点，则${（\overrightarrow{BP}）^2}-\overrightarrow{AP}•\overrightarrow{BC}$的取值范围是（　　）

A．

$[\frac{1}{4}，3]$

B．

$[\frac{1}{2}，5]$

C．

$[\frac{13}{4}，5]$

D．

$[-\frac{27}{4}，-5]$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．用量词符号“?”或“?”表示下列命题：
（1）不论m取何实数，方程x²+x-m=0必有实数根：?m∈R，方程x²+x-m=0必有实数根；
（2）存在一个有理数x₀，使得x₀²=8：?x₀∈Q，使得x₀²=8．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．

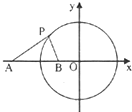已知圆C：x²+y²=9，点A（-5，0），直线l：x-2y=0．
（1）求与圆C相切，且与直线l垂直的直线方程；
（2）在x轴上是否存在定点B（不同于点A），使得对于圆C上任一点P，都有$\frac{|PB|}{|PA|}$为常数？若存在，试求所有满足条件的点B的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．已知等差数列{a_n}（n∈N^*）的前n项和为S_n，且a₃=5，S₃=9
（1）求数列{a_n}的通项公式；
（2）若${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$，求数列{b_n}的前n项和T_n；
（3）若等比数列{c_n}（n∈N*）中，c₂=a₂，c₃=a₅，求数列{c_n}的前n项和Q_n．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．已知f（x）=3sin（2x-$\frac{π}{3}$）+1，x∈R．
（1）求函数f（x）的最小正周期和单调增区间；
（2）函数f（x）的图象可以由函数y=sinx（x∈R）的图象经过怎样变换得到？
（3）求f（x）的最大值及取最大值时x的值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．下列各项中，值等于$\frac{1}{2}$的是（　　）

	A．	cos45°cos15°+sin45°sin15°		B．	$\sqrt{\frac{{1-cos\frac{π}{6}}}{2}}$
	C．	cos²$\frac{π}{12}$-sin²$\frac{π}{12}$		D．	$\frac{{tan{{22.5}°}}}{{1-{{tan}^2}{{22.5}°}}}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．

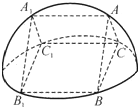如图，直三棱柱ABC-A₁B₁C₁的六个顶点都在半径为1的半球面上，AB=AC，侧面BCC₁B₁是半球底面圆的内接正方形，则侧面ABB₁A₁的面积为$\sqrt{2}$．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学