
(本小题满分14分)
设函数 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 在
在 上的最大值;
上的最大值;
(Ⅲ)当 时,
时, 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) 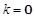 (2)
(2) 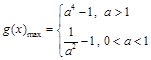 (3)
(3) 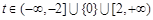
解析试题分析:(Ⅰ)由 得
得 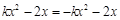 ,
,
∴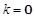 .································· 2分
.································· 2分
(Ⅱ)∵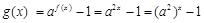 ·················· 3分
·················· 3分
①当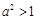 ,即
,即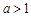 时,
时,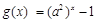 在
在 上为增函数,
上为增函数,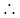
 最大值为
最大值为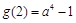 .······················· 5分
.······················· 5分
②当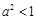 ,即
,即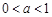 时,
时,
∴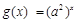 在
在 上为减函数,
上为减函数,
∴ 最大值为
最大值为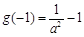 .······················· 7分
.······················· 7分
∴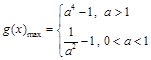 ························· 8分
························· 8分
(Ⅲ)由(Ⅱ)得 在
在 上的最大值为
上的最大值为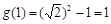 ,
,
∴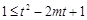 即
即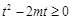 在
在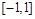 上恒成立················ 10分
上恒成立················ 10分
令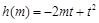 ,
,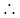
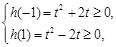
即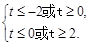
所以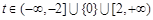 . 14分
. 14分
考点:本试题主要是考查了二次函数的性质以及不等式恒成立问题的运用。
点评:对于二次函数的性质主要是对称性的运用,同时遇到不等式的恒成立问题,一般要采用分离参数的思想来得到其取值范围。属于中档题,有一定的难度。


科目:高中数学 来源: 题型:解答题
(本小题14分)已知函数 ,设
,设 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。
(Ⅲ)是否存在实数 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说名理由。
的取值范围,若不存在,说名理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分8分)
某商店经营的消费品进价每件14元,月销售量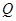 (百件)与销售价格
(百件)与销售价格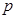 (元)的关系如下图,每月各种开支2000元.
(元)的关系如下图,每月各种开支2000元.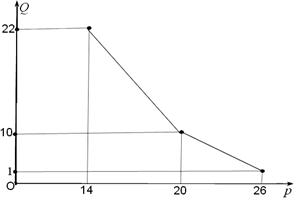
(1)写出月销售量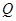 (百件)与销售价格
(百件)与销售价格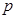 (元)的函数关系;
(元)的函数关系;
(2)写出月利润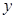 (元)与销售价格
(元)与销售价格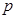 (元)的函数关系;
(元)的函数关系;
(3)当商品价格每件为多少元时,月利润最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设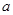 ∈R,函数
∈R,函数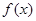 =
=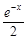 (
(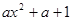 ),其中e是自然对数的底数.
),其中e是自然对数的底数.
(1)判断f (x)在R上的单调性;
(2)当– 1 <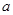 < 0时,求f (x)在[1,2]上的最小值.
< 0时,求f (x)在[1,2]上的最小值.
选做题:请考生从给出的3道题中任选一题做答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com