
分析 (1)由点A到F1,F2两点的距离之和等于4.可得2a=4,解得a.又点$A(1,\;\;\frac{3}{2})$在椭圆上,可得 $\frac{1}{4}+\frac{9}{{4{b^2}}}=1$,解得b2,即可得出.
(2)$c=\sqrt{{a}^{2}-{b}^{2}}$=1.记|KF1|=m,|KF2|=n,则m+n=4,由余弦定理可得:$|{F_1}{F_2}{|^2}\;={(2c)^2}={m^2}+{n^2}-2mncos{30°}$,可得mn.利用 ${S_{△{F_1}K{F_2}}}=\frac{1}{2}mnsinα=\frac{1}{4}mn$,即可得出.
解答 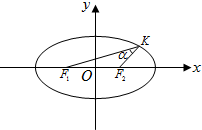 解:(1)∵点A到F1,F2两点的距离之和等于4.
解:(1)∵点A到F1,F2两点的距离之和等于4.
∴2a=4,解得 a=2.
又点$A(1,\;\;\frac{3}{2})$在椭圆上,∴$\frac{1}{4}+\frac{9}{{4{b^2}}}=1$,解得b2=3,
所以所求椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)$c=\sqrt{{a}^{2}-{b}^{2}}$=1.
记|KF1|=m,|KF2|=n,则m+n=4,
由余弦定理可得:$|{F_1}{F_2}{|^2}\;={(2c)^2}={m^2}+{n^2}-2mncos{30°}$,
∴${(2c)^2}={m^2}+{n^2}-\sqrt{3}\;mn$,
${(2c)^2}={(m+n)^2}-(2+\sqrt{3}\;)\;mn$,
∴$mn\;=12(2-\sqrt{3})$,
又 ${S_{△{F_1}K{F_2}}}=\frac{1}{2}mnsinα=\frac{1}{4}mn$,
∴${S_{△{F_1}K{F_2}}}=3\;(\;2-\sqrt{3}\;)$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、三角形面积计算公式、余弦定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
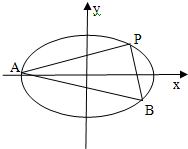 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,1),且两焦点与短轴的一个端点构成等腰直角三角形.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,1),且两焦点与短轴的一个端点构成等腰直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com