
分析 (1)由题意可得an+1-1=an2-2an+1=${({a}_{n}-1)}^{2}$,结合条件代入$\frac{ln({a}_{n+1}-1)}{ln({a}_{n}-1)}$化简,由等比数列的定义证明数列{ln(an-1)}是等比数列;
(2)由(1)和等比数列的通项公式求出ln(an-1),由对数的运算求出an,再化简an+1=an2-2an+2得$\frac{1}{{a}_{n+1}-2}=\frac{1}{{{a}_{n}(a}_{n}-2)}$,裂项后求出$\frac{1}{{a}_{n}}$并代入bn=$\frac{1}{{a}_{n}}$+$\frac{1}{{a}_{n}-2}$,利用裂项相消法求出Sn,即可证明结论.
解答 证明:(1)由题意得,an+1=an2-2an+2,an>0,
∴an+1-1=an2-2an+1=${({a}_{n}-1)}^{2}$,
由a1=3得,a1-1=3-1=2,
∴$\frac{ln({a}_{n+1}-1)}{ln({a}_{n}-1)}$=$\frac{ln({a}_{n}-1)^{2}}{ln({a}_{n}-1)}$=$\frac{2ln({a}_{n}-1)}{ln({a}_{n}-1)}$=2,
∴数列{ln(an-1)}是以2为公比、ln2为首项的等比数列;
(2)由(1)得,ln(an-1)=ln2•2n-1,
则an-1=${e}^{ln2•{2}^{n-1}}$=${2}^{{2}^{n-1}}$,即an=${2}^{{2}^{n-1}}$+1,
∵an+1=an2-2an+2,∴an+1-2=an(an-2),
则$\frac{1}{{a}_{n+1}-2}=\frac{1}{{{a}_{n}(a}_{n}-2)}$=$\frac{1}{2}$($\frac{1}{{a}_{n}-2}-\frac{1}{{a}_{n}}$),
∴$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}-2}-\frac{2}{{a}_{n+1}-2}$,
∴bn=$\frac{1}{{a}_{n}}$+$\frac{1}{{a}_{n}-2}$=$\frac{2}{{a}_{n}-2}-\frac{2}{{a}_{n+1}-2}$,
∴Sn=b1+b2+…+bn=($\frac{2}{{a}_{1}-2}-\frac{2}{{a}_{2}-2}$)+($\frac{2}{{a}_{2}-2}-\frac{2}{{a}_{3}-2}$)+…+($\frac{2}{{a}_{n}-2}-\frac{2}{{a}_{n+1}-2}$)
=$\frac{2}{{a}_{1}-2}-\frac{2}{{a}_{n+1}-2}$=$2-\frac{2}{{2}^{{2}^{n}}-1}$<2,
即Sn<2成立.
点评 本题考查数列的递推公式的化简、变形,等比数列的定义、通项公式,对数的运算性质,以及裂项相消法求数列的和,比较综合、难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
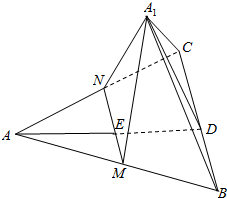 如图,AD为△ABC的边BC上的高,E在AD上,且ED=2AE,过E作直线MN∥BC,分别交AB,AC于M,N点,将△AMN沿MN折起到A1MN,使二面角A1-MN-C为60°,求证:平面A1MN⊥平面A1BC.
如图,AD为△ABC的边BC上的高,E在AD上,且ED=2AE,过E作直线MN∥BC,分别交AB,AC于M,N点,将△AMN沿MN折起到A1MN,使二面角A1-MN-C为60°,求证:平面A1MN⊥平面A1BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
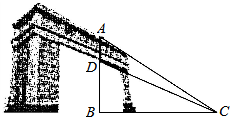 某大学的大门蔚为壮观,有个学生想搞清楚门洞拱顶D到其正上方A点的距离,他站在地面C处,利用皮尺量得BC=9米,利用测角仪测得仰角∠ACB=45°,测得仰角∠BCD后通过计算得到sin∠ACD=$\frac{\sqrt{26}}{26}$,则AD的距离为( )
某大学的大门蔚为壮观,有个学生想搞清楚门洞拱顶D到其正上方A点的距离,他站在地面C处,利用皮尺量得BC=9米,利用测角仪测得仰角∠ACB=45°,测得仰角∠BCD后通过计算得到sin∠ACD=$\frac{\sqrt{26}}{26}$,则AD的距离为( )| A. | 2米 | B. | 2.5米 | C. | 3米 | D. | 4米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
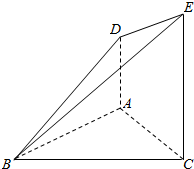 如图所示,AD⊥平面ABC,CE⊥平面ABC,CE=2AD,AC=AB=1,BC=$\sqrt{2}$,证明:
如图所示,AD⊥平面ABC,CE⊥平面ABC,CE=2AD,AC=AB=1,BC=$\sqrt{2}$,证明:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com