
分析 从早10点开始计时,设甲经过x分钟到达,乙经过y分钟到达,可得x、y满足的不等式线组对应的平面区域为如图的正方形OABC,而甲乙能够见面,x、y满足的平面区域是图中的六边形OEFBGH.分别算出图中正方形和六边形的面积,相除即可得到两人能见面的概率.
解答 解:从早10点开始计时,设甲经过x分钟到达,乙经过y分钟到达,则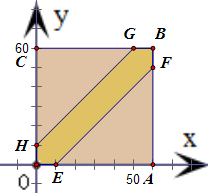
x、y满足$\left\{\begin{array}{l}{0≤x≤60}\\{0≤y≤60}\end{array}\right.$,作出不等式组对应的平面区域,
得到图中的正方形OABC,
若甲乙能够见面,则x、y满足|x-y|≤10,
该不等式对应的平面区域是图中的六边形OEFBGH
∵S正方形OABC=60×60=3600,
S六边形OEFBGH=S正方形OABC-2S△AEF=1100
因此,甲乙能见面的概率P=$\frac{11}{36}$.
故答案为:$\frac{11}{36}$.
点评 本题给出两人相约,求它们能碰面的概率.着重考查了几何概型及其计算公式等知识,属于基础题.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
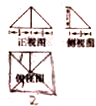
 如图,是一个几何体的三视图,其中主视图、左视图是直角边长为2的等腰直角三角形,俯视图为边长为2的正方形,则此几何体的表面积为( )
如图,是一个几何体的三视图,其中主视图、左视图是直角边长为2的等腰直角三角形,俯视图为边长为2的正方形,则此几何体的表面积为( )| A. | 8+4$\sqrt{2}$ | B. | 8+4$\sqrt{3}$ | C. | $6+6\sqrt{2}$ | D. | 8+2$\sqrt{2}$+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | $\frac{8π}{3}$ | C. | 4π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,O是边长为2的等边△ABC的中心,动点E在边AC上运动,F在边AB及BC上运动,则$\overrightarrow{OB}$•$\overrightarrow{EF}$的取值范围是[0,2].
如图,O是边长为2的等边△ABC的中心,动点E在边AC上运动,F在边AB及BC上运动,则$\overrightarrow{OB}$•$\overrightarrow{EF}$的取值范围是[0,2].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com