练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)是定义域为R的奇函数，且在(－∞，0)内的零点有2012个，则f(x)的零点的个数为________．


    4025

    [解析]　因为f(x)为奇函数，且在(－∞，0)内有2012个零点，由奇函数的对称性知，在(0，＋∞)内也有2012个零点，又x∈R，所以f(0)＝0，因此共4025个零点．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若函数y＝的定义域为R，则实数k的取值范围为(　　)

    A．(0，)                             B．(，＋∞)

    C．(－∞，0)                           D．[0，)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知一元二次不等式f(x)<0的解集为{x|x<－1或x>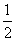}，则f(10x)>0的解集为(　　)

    A．{x|x<－1或x>－lg2}               B．{x|－1<x<－lg2}

    C．{x|x>－lg2}                       D．{x|x<－lg2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    方程lgx＋x＝0的根所在区间是(　　)

    A．(－∞，0)　　　　　　               B．(0,1)

    C．(1,2)                               D．(2,4)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某商品零售价2014年比2013年上涨25%，欲控制2015年比2013年只上涨10%，则2015年应比2014年降价(　　)

    A．15%                                 B．12%

    C．10%                                 D．50%

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某公司从2004年的年产值100万元，增加到10年后2014年的500万元，如果每年产值增长率相同，则每年的平均增长率是多少？(ln(1＋x)≈x，lg2＝0.3，ln10＝2.30)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在斜三角形ABC中，sinA＝－cosB·cosC，且tanB·tanC＝1－，则角A的值为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝cos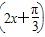＋sin2x.

    (1)求函数f(x)的最大值和最小正周期；

    (2)设A、B、C为△ABC的三个内角，若cosB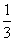＝，f(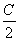)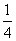＝－，且C为锐角，求sinA的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有一长为1的斜坡，它的倾斜角为20°，现高不变，将倾斜角改为10°，则斜坡长为(　　)

    A．1                                                             B．2sin10°

    C．2cos10°                                                   D．cos20°

    查看答案和解析>>

    同步练习册答案