
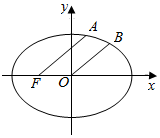
 如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )
如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 设出A的坐标,由题意方程求得F的坐标及椭圆的离心率,由焦半径公式求得|AF|,求出AF的斜率,得到OB的方程,联立OB方程与椭圆方程,求出B的坐标,得到|OB|,结合|FA|:|OB|=3:2列式求得答案.
解答 解:设A(x0,y0),
∵A(x0,y0)在椭圆上,∴$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}=1$,
由椭圆方程为$\frac{{x}^{2}}{2}$+y2=1得,a2=2,b2=1,
∴c2=a2-b2=2-1=1,则c=1,
∴F(-1,0),e=$\frac{c}{a}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,
则|AF|=$\sqrt{2}+\frac{\sqrt{2}}{2}{x}_{0}$,
又${k}_{AF}=\frac{{y}_{0}}{{x}_{0}+1}$,且FA∥OB,∴${k}_{OB}=\frac{{y}_{0}}{{x}_{0}+1}$,
∴OB所在直线方程为$y=\frac{{y}_{0}}{{x}_{0}+1}x$,
联立$\left\{\begin{array}{l}{y=\frac{{y}_{0}}{{x}_{0}+1}x}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}^{2}=\frac{2({x}_{0}+1)^{2}}{2{{y}_{0}}^{2}+({x}_{0}+1)^{2}}}\\{{y}^{2}=\frac{2{{y}_{0}}^{2}}{2{{y}_{0}}^{2}+({x}_{0}+1)^{2}}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}^{2}=\frac{2({x}_{0}+1)^{2}}{2{x}_{0}+3}}\\{{y}^{2}=\frac{2-{{x}_{0}}^{2}}{2{x}_{0}+3}}\end{array}\right.$,
则|OB|=$\sqrt{{x}^{2}+{y}^{2}}=\sqrt{\frac{2({x}_{0}+1)^{2}}{2{x}_{0}+3}+\frac{2-{{x}_{0}}^{2}}{2{x}_{0}+3}}$=$\sqrt{\frac{({x}_{0}+2)^{2}}{2{x}_{0}+3}}$,
由|FA|:|OB|=3:2,
得$\frac{\sqrt{2}+\frac{\sqrt{2}}{2}{x}_{0}}{\sqrt{\frac{({x}_{0}+2)^{2}}{2{x}_{0}+3}}}=\frac{3}{2}$,解得:${x}_{0}=\frac{3}{4}$.
故选:B.
点评 本题考查椭圆的简单性质,考查了椭圆焦半径公式的应用,考查运算能力,是中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
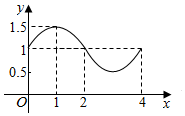 函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )| A. | f(x)=$\frac{1}{2}$sin2πx+1,S=2016 | B. | f(x)=$\frac{1}{2}$sin2πx+1,S=2016$\frac{1}{2}$ | ||
| C. | f(x)=$\frac{1}{2}$sin$\frac{π}{2}$x+1,S=2017$\frac{1}{2}$ | D. | f(x)=$\frac{1}{2}$sin$\frac{π}{2}$x+1,S=2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q是真命题 | B. | p∧(﹁q)是真命题 | C. | ﹁p∧q是真命题 | D. | ﹁p∧﹁q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com