
ЁОЬтФПЁПШчЭМЃЌ![]() ЕФжБНЧБпOAдкxжсЩЯЃЌЖЅЕуBЕФзјБъЮЊ
ЕФжБНЧБпOAдкxжсЩЯЃЌЖЅЕуBЕФзјБъЮЊ![]() ЃЌжБЯпCDНЛABгкЕу
ЃЌжБЯпCDНЛABгкЕу![]() ЃЌНЛxжсгкЕу
ЃЌНЛxжсгкЕу![]() .
.

(1)ЧѓжБЯпCDЕФЗНГЬЃЛ
(2)ЖЏЕуPдкxжсЩЯДгЕу![]() ГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђxжсе§ЗНЯђдЫЖЏЃЌЙ§ЕуPзїжБЯпlДЙжБгкxжсЃЌЩшдЫЖЏЪБМфЮЊt.
ГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђxжсе§ЗНЯђдЫЖЏЃЌЙ§ЕуPзїжБЯпlДЙжБгкxжсЃЌЩшдЫЖЏЪБМфЮЊt.
ЂйЕуPдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГИіЮЛжУЃЌЪЙЕУ![]() ?ШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
?ШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЂкЧыЬНЫїЕБtЮЊКЮжЕЪБЃЌдкжБЯпlЩЯДцдкЕуMЃЌдкжБЯпCDЩЯДцдкЕуQЃЌЪЙЕУвдOBЮЊвЛБпЃЌOЃЌBЃЌMЃЌQЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌВЂЧѓГіДЫЪБtЕФжЕ.
ЁОД№АИЁП(1)![]() ЃЛ(2)ЂйТњзуЬѕМўЕФЕуPзјБъЮЊ
ЃЛ(2)ЂйТњзуЬѕМўЕФЕуPзјБъЮЊ![]() Лђ
Лђ![]() ЃЌЂкТњзуЬѕМўЕФtЕФжЕЮЊ
ЃЌЂкТњзуЬѕМўЕФtЕФжЕЮЊ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУСНЕуЪНЧѓГіжБЯпЗНГЬЃЌдйЛЏЮЊвЛАуЗНГЬЃЛ
ЃЈ2ЃЉЂйИљОнЬтвтзїDPЁЮOBЃЌРћгУЯрЫЦШ§НЧаЮЧѓГіЕуPЕФзјБъЃЌИљОнЖдГЦадЧѓЕУPЁфЕФзјБъЃЛ
ЂкЗжЧщПіЬжТлЃЌOPЃНOBЃН10ЪБЃЌзїPQЁЮOBНЛCDгкQЃЌЧѓЕУЕуMгыЕуPжиКЯЃЌtЃН0ЃЛ
OQЃНOBЪБЃЌЧѓГіЕуQЕФКсзјБъЃЌМЦЫуMЕФКсзјБъЃЌЧѓЕУtЕФжЕЃЛQЕугыCЕужиКЯЪБЃЌЧѓЕУMЕуЕФКсзјБъЃЌЕУГіtЕФжЕ.
НтЃКЃЈ1ЃЉжБЯпCDЙ§ЕуCЃЈ12ЃЌ0ЃЉЃЌDЃЈ6ЃЌ3ЃЉЃЌ
жБЯпЗНГЬЮЊ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЛЏЮЊвЛАуаЮЪНЪЧx+2yЉ12ЃН0ЃЛ
ЃЈ2ЃЉЂйШчЭМ1жаЃЌ
зїDPЁЮOBЃЌдђЁЯPDAЃНЁЯBЃЌ
гЩDPЁЮOBЕУЃЌ![]() ЃН
ЃН![]() ЃЌМД
ЃЌМД![]() ЃН
ЃН![]() ЃЌЁрPAЃН
ЃЌЁрPAЃН![]() ЃЛ
ЃЛ
ЁрOPЃН6Љ![]() ЃН
ЃН![]() ЃЌЁрЕуPЃЈ
ЃЌЁрЕуPЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ИљОнЖдГЦаджЊЃЌЕБAPЃНAPЁфЪБЃЌPЁфЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁрТњзуЬѕМўЕФЕуPзјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЂкШчЭМ2жаЃЌЕБOPЃНOBЃН10ЪБЃЌзїPQЁЮOBНЛCDгкQЃЌ
дђжБЯпOBЕФНтЮіЪНЮЊyЃН![]() xЃЌ
xЃЌ
жБЯпPQЕФНтЮіЪНЮЊyЃН![]() x+
x+![]() ЃЌ
ЃЌ
гЩ ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌЁрQЃЈЉ4ЃЌ8ЃЉЃЛ
ЃЌЁрQЃЈЉ4ЃЌ8ЃЉЃЛ
ЁрPQЃН![]() ЃН10ЃЌ
ЃН10ЃЌ
ЁрPQЃНOBЃЌЁрЫФБпаЮOPQBЪЧЦНааЫФБпаЮЃЌ
гжOPЃНOBЃЌЁрЦНааЫФБпаЮOPQBЪЧСтаЮЃЛ
ДЫЪБЕуMгыЕуPжиКЯЃЌЧвtЃН0ЃЛ
ШчЭМ3ЃЌЕБOQЃНOBЪБЃЌЩшQЃЈmЃЌЉ![]() m+6ЃЉЃЌ
m+6ЃЉЃЌ
дђгаm2+ ЃН102ЃЌ
ЃН102ЃЌ
НтЕУmЃН![]() ЃЛ
ЃЛ
ЁрЕуQЕФКсзјБъЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЩшMЕФКсзјБъЮЊaЃЌ
дђ![]() ЃН
ЃН Лђ
Лђ![]() ЃН
ЃН ЃЌ
ЃЌ
НтЕУaЃН![]() ЛђaЃН
ЛђaЃН![]() ЃЛ
ЃЛ
гжЕуPЪЧДгЕуЃЈЉ10ЃЌ0ЃЉПЊЪМдЫЖЏЃЌ
дђТњзуЬѕМўЕФtЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ШчЭМ4ЃЌЕБQЕугыCЕужиКЯЪБЃЌMЕуЕФКсзјБъЮЊ6ЃЌДЫЪБtЃН16ЃЛ
злЩЯЃЌТњзуЬѕМўЕФtжЕЮЊ0ЃЌЛђ16ЃЌЛђ![]() Лђ
Лђ![]() .
.






 зДдЊМАЕкЯЕСаД№АИ
зДдЊМАЕкЯЕСаД№АИ ЭЌВНАТЪ§ЯЕСаД№АИ
ЭЌВНАТЪ§ЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
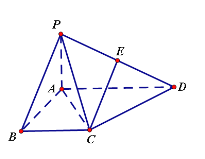
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ![]() ЃЌЕзУц
ЃЌЕзУц![]() ЪЧжБНЧЬнаЮЃЌ
ЪЧжБНЧЬнаЮЃЌ![]() .
.
ЃЈЂёЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂђЃЉдкРт![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() //ЦНУц
//ЦНУц![]() ЃПШєДцдкЃЌЧыШЗЖЈ
ЃПШєДцдкЃЌЧыШЗЖЈ![]() ЕуЕФЮЛжУЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕуЕФЮЛжУЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§ЯюЪ§Са![]() ЕФЧАnЯюКЭ
ЕФЧАnЯюКЭ![]() Тњзу
Тњзу![]()
ЃЈ1ЃЉЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉШє ЃЈnЁЪN*ЃЉЃЌЧѓЪ§Са
ЃЈnЁЪN*ЃЉЃЌЧѓЪ§Са![]() ЕФЧАnЯюКЭ
ЕФЧАnЯюКЭ![]() ;
;
ЃЈ3ЃЉЪЧЗёДцдкЪЕЪ§![]() ЪЙЕУ
ЪЙЕУ![]() Жд
Жд![]() КуГЩСЂЃЌШєДцдкЃЌЧѓЪЕЪ§
КуГЩСЂЃЌШєДцдкЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЌШєВЛДцдкЫЕУїРэгЩЃЎ
ЕФШЁжЕЗЖЮЇЃЌШєВЛДцдкЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЕМфзтСоМзЁЂввСНжжЩшБИЩњВњAЃЌBСНРрВњЦЗЃЌМзжжЩшБИУПЬьФмЩњВњAРрВњЦЗ8МўКЭBРрВњЦЗ15МўЃЌввжжЩшБИУПЬьФмЩњВњAРрВњЦЗ10МўКЭBРрВњЦЗ25МўЃЌвбжЊЩшБИМзУПЬьЕФзтСоЗб300дЊЃЌЩшБИввУПЬьЕФзтСоЗб400дЊЃЌЯжГЕМфжСЩйвЊЩњВњAРрВњЦЗ100МўЃЌBРрВњЦЗ200МўЃЌЫљашзтСоЗбзюЩйЮЊ__дЊ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЭждВ![]() ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ
ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЙ§
ЃЌЙ§![]() ЕФжБЯпНЛЭждВгк
ЕФжБЯпНЛЭждВгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌШєЭждВ
СНЕуЃЌШєЭждВ![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌ
ЃЌ![]() ЕФжмГЄЮЊ16ЃЎ
ЕФжмГЄЮЊ16ЃЎ
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшВЛОЙ§ЭждВЕФжааФЖјЦНаагкЯв![]() ЕФжБЯпНЛЭждВ
ЕФжБЯпНЛЭждВ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌЩшЯв
ЃЌЩшЯв![]() ЃЌ
ЃЌ![]() ЕФжаЕуЗжБ№ЮЊ
ЕФжаЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЎжЄУїЃК
ЃЎжЄУїЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕуЙВЯпЃЎ
Ш§ЕуЙВЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтзЖ![]() жаЃЌ
жаЃЌ![]() ЦНУц
ЦНУц![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЕФжаЕу.
ЕФжаЕу.

ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєFдкЯпЖЮ![]() ЩЯЃЌТњзу
ЩЯЃЌТњзу![]() ЦНУц
ЦНУц![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєШ§НЧаЮ![]() ЪЧе§Ш§НЧаЮЃЌБпГЄЮЊ2ЃЌЧѓЖўУцНЧ
ЪЧе§Ш§НЧаЮЃЌБпГЄЮЊ2ЃЌЧѓЖўУцНЧ![]() ЕФе§ЧажЕ.
ЕФе§ЧажЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЫЋЧњЯпC1ЃК![]() -
-![]() =1ЃЎ
=1ЃЎ
ЃЈ1ЃЉШєЕуMЃЈ3ЃЌtЃЉдкЫЋЧњЯпC1ЩЯЃЌЧѓMЕуЕНЫЋЧњЯпC1гвНЙЕуЕФОрРыЃЛ
ЃЈ2ЃЉЧѓгыЫЋЧњЯпC1гаЙВЭЌНЅНќЯпЃЌЧвЙ§ЕуЃЈ-3ЃЌ2![]() ЃЉЕФЫЋЧњЯпC2ЕФБъзМЗНГЬЃЎ
ЃЉЕФЫЋЧњЯпC2ЕФБъзМЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
ЃЈ![]() ЃЉЕБ
ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФЕЅЕїЧјМфКЭМЋжЕ.
ЕФЕЅЕїЧјМфКЭМЋжЕ.
ЃЈ![]() ЃЉШєЖдгкШЮвт
ЃЉШєЖдгкШЮвт![]() ЃЌЖМга
ЃЌЖМга![]() ГЩСЂЃЌЧѓ
ГЩСЂЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ ЃЛ
ЕФШЁжЕЗЖЮЇ ЃЛ
ЃЈ![]() ЃЉШє
ЃЉШє![]() Чв
Чв![]() жЄУїЃК
жЄУїЃК![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com