考点:利用导数研究函数的单调性,绝对值不等式的解法
专题:导数的综合应用
分析:(1)当a=-4时,f′(x)=
,(x>0),令f′(x)≥0,令f′(x)<0,从而函数f(x)的单调增区间为[
,+∞)单调减区间为(0,
),
(2)f′(x)=2x-
+
,得|2+
-
|>1,从而有2+
-
>1恒成立,只需证明:x
1 x
2+
≥a即可,对此:设t=
,t>0,u(t)=t
2+
,而u(t)=t
2+
+
≥3
=
>4≥a,故命题得证.
解答:
解:(1)当a=-4时,f′(x)=
,(x>0),
令f′(x)≥0,即:x
3-2x-1≥0,(x+1)(x
2-x-1)≥0,解得:x≥
,
令f′(x)<0,解得:0<x<
,
∴函数f(x)的单调增区间为[
,+∞)单调减区间为(0,
),
(2)f′(x)=2x-
+
,
∴|f′(x
1 )-f′(x
2 )|=|x
1-x
2||2+
-
|,
∴|2+
-
|>1
下面证明?x
1,x
2∈(0,+∞),x
1≠x
2,
有2+
-
>1恒成立,
即证:a<x
1x
2+
成立,
∵x
1x
2+
>x
1 x
2+
,
∴只需证明:x
1 x
2+
≥a即可,
对此:设t=
,t>0,u(t)=t
2+
,
而u(t)=t
2+
+
≥3
=
>4≥a,
∴即证:a<x
1x
2+
成立,
∴a<x
1x
2+
.
故命题得证.
点评:本题考察了函数的单调性,导数的应用,不等式的证明,是一道综合题.



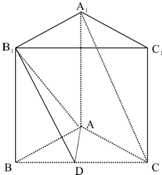 如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.
如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.