
分析 (1)由|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$夹角为120°,利用数量积的定义可得$\overrightarrow{a}•\overrightarrow{b}$=-4.由于($\overrightarrow{a}$+λ$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-3$\overrightarrow{b}$),可得($\overrightarrow{a}$+λ$\overrightarrow{b}$)•(2$\overrightarrow{a}$-3$\overrightarrow{b}$)=0,代入解出即可.
(2)不妨设$\overrightarrow{a}$=(4,0),$\overrightarrow{b}$=$(-1,\sqrt{3})$,$\overrightarrow{c}$=(cosθ,sinθ).可得$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$=$2\sqrt{3}$$sin(θ+\frac{π}{3})$≤2$\sqrt{3}$,即可得出.
解答 解:(1)∵|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$夹角为120°,∴$\overrightarrow{a}•\overrightarrow{b}$=4×2×cos120°=-4.
∵($\overrightarrow{a}$+λ$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-3$\overrightarrow{b}$),
∴($\overrightarrow{a}$+λ$\overrightarrow{b}$)•(2$\overrightarrow{a}$-3$\overrightarrow{b}$)=$2{\overrightarrow{a}}^{2}-3λ{\overrightarrow{b}}^{2}$+$(2λ-3)\overrightarrow{a}•\overrightarrow{b}$=2×42-3λ×22+(2λ-3)×(-4)=0,
解得λ=$\frac{11}{5}$.
(2)不妨设$\overrightarrow{a}$=(4,0),$\overrightarrow{b}$=$(-1,\sqrt{3})$,$\overrightarrow{c}$=(cosθ,sinθ).
则$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$=3cosθ+$\sqrt{3}$sinθ=$2\sqrt{3}$$sin(θ+\frac{π}{3})$≤2$\sqrt{3}$,当$sin(θ+\frac{π}{3})$=1时取等号.
∴$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$的最大值为2$\sqrt{3}$.
点评 本题考查了数量积的定义及其运算性质、向量垂直与数量积的关系、三角函数的值域,考查了推理能力与计算能力,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | a$>\frac{1}{4}$ | B. | a$≥\frac{1}{4}$ | C. | a$<\frac{1}{4}$ | D. | a$≤\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)在R上是奇函数,且当x>0时,f(x)=x2-4x+3.
已知函数f(x)在R上是奇函数,且当x>0时,f(x)=x2-4x+3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
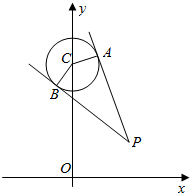 已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)
已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com