
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)已知![]() 在定义域上为减函数,若对任意的
在定义域上为减函数,若对任意的![]() ,不等式
,不等式![]() 为常数)恒成立,求
为常数)恒成立,求![]() 的取值范围.
的取值范围.
【答案】解:(1)因为![]() 是奇函数,所以
是奇函数,所以![]() =0,
=0,
即![]() ………………………3
………………………3
(2)由(1)知![]() ,………………………5
,………………………5
设![]()
![]() ,则
,则![]() .
.
因为函数y=2![]() 在R上是增函数且
在R上是增函数且![]() , ∴
, ∴![]() >0.
>0.
又![]() >0 ,∴
>0 ,∴![]() >0,即
>0,即![]() ,
,
∴![]() 在
在![]() 上为减函数.另法:或证明f′(x)
上为减函数.另法:或证明f′(x)![]() 0………………………9
0………………………9
(3)因为![]() 是奇函数,从而不等式
是奇函数,从而不等式
![]() 等价于
等价于![]() ,………………………3
,………………………3
因为![]() 为减函数,由上式推得
为减函数,由上式推得![]() .即对一切
.即对一切![]() 有
有![]() ,
,
从而判别式![]() ………………………13
………………………13
【解析】
定义域为R的奇函数![]() ,得b=1,在代入1,-1,函数值相反得a;
,得b=1,在代入1,-1,函数值相反得a;
![]()
![]() ,通常用函数的单调性转化为自变量的大小关系。
,通常用函数的单调性转化为自变量的大小关系。
(1)![]()
![]() 是奇函数,
是奇函数,![]()
![]() ,┈┈┈┈┈┈┈┈┈┈┈┈2分
,┈┈┈┈┈┈┈┈┈┈┈┈2分
即![]()
![]()
![]()
![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分
![]()
![]()
![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分
![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分
(2)由(1)知![]()
由上式易知![]() 在R上为减函数。 ┈┈┈┈┈┈┈┈┈┈┈┈2分
在R上为减函数。 ┈┈┈┈┈┈┈┈┈┈┈┈2分
又因为![]() 为奇函数,从而不等式
为奇函数,从而不等式![]() ,
,
等价于![]() ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分
![]()
![]() 为减函数
为减函数![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分
即对一切![]() 都有
都有![]() ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分
![]()
![]()
![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分


科目:高中数学 来源: 题型:
【题目】已知双曲线的焦点在x轴上,焦距为![]() ,实轴长为2
,实轴长为2
(1)求双曲线的标准方程与渐近线方程。
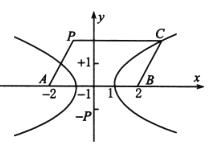
(2)若点 ![]() 在该双曲线上运动,且
在该双曲线上运动,且![]() ,
,![]() ,求以
,求以 ![]() ,
,![]() 为相邻两边的平行四边形
为相邻两边的平行四边形 ![]() 的顶点
的顶点 ![]() 的轨迹.
的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() 与
与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() .记过
.记过![]() 、
、![]() 、
、![]() 三点的圆为圆
三点的圆为圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求过点![]() 与圆
与圆![]() 相交所得弦长为8的直线方程.
相交所得弦长为8的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,若
,若![]() 且
且![]() 时,有
时,有![]() 成立.
成立.
(1)判断![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)解不等式![]() ;
;
(3)若![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级设计了一个实验学科的能力考查方案:考生从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题.规定:至少正确完成其中2道题的便可通过该学科的能力考查.已知6道备选题中考生甲能正确完成其中4道题,另2道题不能完成;考生乙正确完成每道题的概率都为![]() .
.
(Ⅰ)分别求考生甲、乙能通过该实验学科能力考查的概率;
(Ⅱ)记所抽取的3道题中,考生甲能正确完成的题数为![]() ,写出
,写出![]() 的概率分布列,并求
的概率分布列,并求![]() 及
及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县城出租车的收费标准是:起步价是![]() 元(乘车不超过
元(乘车不超过![]() 千米);行驶
千米);行驶![]() 千米后,每千米车费1.2元;行驶
千米后,每千米车费1.2元;行驶![]() 千米后,每千米车费1.8元.
千米后,每千米车费1.8元.
(1)写出车费与路程的关系式;
(2)一顾客计划行程![]() 千米,为了省钱,他设计了三种乘车方案:
千米,为了省钱,他设计了三种乘车方案:
①不换车:乘一辆出租车行![]() 千米;
千米;
②分两段乘车:先乘一辆车行![]() 千米,换乘另一辆车再行
千米,换乘另一辆车再行![]() 千米;
千米;
③分三段乘车:每乘![]() 千米换一次车.
千米换一次车.
问哪一种方案最省钱.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为 ![]() ,且椭圆E上一点到两个焦点距离之和为4;l1 , l2是过点P(0,2)且互相垂直的两条直线,l1交E于A,B两点,l2交E交C,D两点,AB,CD的中点分别为M,N.
,且椭圆E上一点到两个焦点距离之和为4;l1 , l2是过点P(0,2)且互相垂直的两条直线,l1交E于A,B两点,l2交E交C,D两点,AB,CD的中点分别为M,N.
(1)求椭圆E的方程;
(2)求l1的斜率k的取值范围;
(3)求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com