练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．在下列四个正方体中，能得出AB⊥CD的是（　　）
    A．B．C．D．

    分析 在A中，推导出线面垂直，从而得到AB⊥CD；在B中，AB与CD成60°角；在C中，AB与CD成45°角；在D中，AB与CD所成角的正切值为$\sqrt{2}$．

    解答 解：在A中，CD⊥BE，CD⊥AE，BE∩AE=E，
    ∴CD⊥平面ABE，又AB?平面ABE，∴AB⊥CD，故A正确；
    在B中，AB与CD成60°角，故B错误；
    在C中，AB与CD成45°角，故C错误；
    在D中，AB与CD所成角的正切值为$\sqrt{2}$，故D错误．
    故选：A．

    点评 本题考查两异面直线垂直的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力，考查化归与转化思想、数形结合思想，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．在△ABC中，角A，B，C的对边分别为a，b，c，已知acosB+bcosA=$\frac{a+b}{2}$，则C的最大值为$\frac{π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．阅读如图所示的程序框图，程序结束时，输出S的值为（　　）
    A．6B．21C．58D．141

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知函数f（x）=（x-1）•ex-kx，曲线y=f（x）上存在两个不同的极值点，则实数k的取值范围是（-$\frac{1}{e}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．附属z满足z=$\frac{3-i}{i}$，则在复平面内，复数z对应的点位于（　　）
    A．第乙象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在△ABC中，已知b=15，c=5$\sqrt{3}$，B=60°，求∠C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

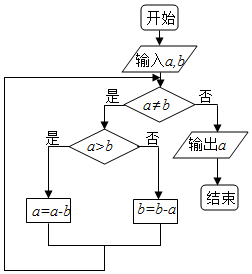    12．《九章算术》是我国古代数学名著，汇集古人智慧，其中的“更相减损术”更是有着深刻的应用．如图所示程序框图的算法思想即来源于此，若输入的a=2016，输出的a=21，则输入的b可能为（　　）
    A．288B．294C．378D．399

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=2cos2x$+\sqrt{3}$sin2x
    （Ⅰ）求f（$\frac{π}{4}$）的值
    （Ⅱ）求f（x）的最小正周期及单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．某公司10位员工的月工资（单位：元）为x1，x2，…x10，其均值和方差分别为$\overline{x}$和s2，若从下月起每位员工的月工次增加200元，则这10位员工下月工资的均值和方差分别为（　　）
    A．$\overline{x}$，s2B．$\overline{x}$+200，s2C．$\overline{x}$，2002s2D．$\overline{x}$+200，s2+2002

    查看答案和解析>>

    同步练习册答案