Question

4．设关于x的一元二次方程为x²+2ax+b²=0．
（1）若a是从-2，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率．
（2）若a是从区间[-3，0]中任取的一个数，b是从区间[-2，0]中任取的一个数，求上述方程有实根的概率．

Answer 1

分析 （1）根据古典概型的概率公式，利用列举法进行求解即可．
（2）作出不等式组对应的平面区域，利用几何概型的概率公式进行求解即可．

解答 解：设事件A为“方程为有实数根”，
事件A发生时a，b满足△=4a²-4b²≥0，就|a|≥|b|，
（1）基本事件共有12个：
（-2，0），（-2，1），（-2，2），
（1，0），（1，1），（1，2），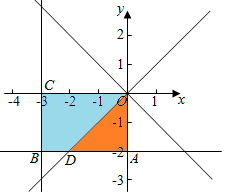
（2，0），（2，1），（2，2），
（3，0），（3，1），（3，2），
其中第一个数表示a，第二个数表示b的取值．事件A包含11个基本事件，
故事件A发生的概率P（A）=$\frac{11}{12}$．
（2）实验的全部结果构成的区域为{（a，b）|$\left\{\begin{array}{l}{-3≤a≤0}\\{-2≤b≤0}\end{array}\right.$}，其面积为6
构成事件A的区域为{（a，b）|$\left\{\begin{array}{l}{-3≤a≤0}\\{-2≤b≤0}\\{|a|≥|b|}\end{array}\right.$}，其面积为4
故事件A发生的概率P（A）=$\frac{4}{6}=\frac{2}{3}$．

点评 本题主要考查概率的计算，涉及古典概型和几何概型的概率公式，利用列举法以及图象法是解决本题的关键．