
分析 (Ⅰ)由双曲线的离心率为$\frac{2}{\sqrt{3}}$,所以椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,又右顶点为(2,0),即a=2,c=$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$,即可得出.
(Ⅱ)设M(x1,y1)、N(x2,y2),可得${x}_{1}^{2}+4{y}_{1}^{2}$=4,${x}_{2}^{2}+4{y}_{2}^{2}$=4.由直线OM与ON的斜率之积为$-\frac{1}{4}$,可得$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=-$\frac{1}{4}$,化为:x1x2+4y1y2=0,由动点P(x0,y0)满足$\overrightarrow{OP}=\overrightarrow{OM}+3\overrightarrow{ON}$,可得x0=x1+3x2,y0=y1+3y2.
代入化简即可得出.
解答 (Ⅰ)解:∵双曲线的离心率为$\frac{2}{\sqrt{3}}$,所以椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
又∵右顶点为(2,0),即a=2,c=$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
∴椭圆方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(Ⅱ)证明:设M(x1,y1)、N(x2,y2),
∴${x}_{1}^{2}+4{y}_{1}^{2}$=4,${x}_{2}^{2}+4{y}_{2}^{2}$=4.
∵直线OM与ON的斜率之积为$-\frac{1}{4}$,∴$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=-$\frac{1}{4}$,化为:x1x2+4y1y2=0,
∵动点P(x0,y0)满足$\overrightarrow{OP}=\overrightarrow{OM}+3\overrightarrow{ON}$,
∴x0=x1+3x2,y0=y1+3y2.
∴${x_0}^2+4{y_0}^2$=$({x}_{1}+3{x}_{2})^{2}$+4$({y}_{1}+3{y}_{2})^{2}$
=${x}_{1}^{2}+4{y}_{1}^{2}$+$9({x}_{2}^{2}+4{y}_{2}^{2})$+6(x1x2+4y1y2)=4+9×4+6×0=40为定值.
点评 本题考查了椭圆与双曲线的标准方程及其性质、点与椭圆的关系、斜率计算公式、斜率坐标运算性质,考查了推理能力与计算能力,属于难题.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
 如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )| A. | (1)和(3) | B. | (2)和(5) | C. | (1)和(4) | D. | (2)和(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
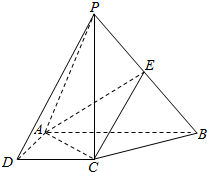 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=$\sqrt{2}$,且PC⊥CD,BC⊥PA,E是PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=$\sqrt{2}$,且PC⊥CD,BC⊥PA,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com