
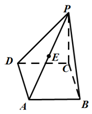 如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.(1)求证:平面EBD⊥平面ABCD;
如图在边长为2的菱形ABCD中,∠ABC=60°,PC⊥平面ABCD,PC=2,E为PA的中点.(1)求证:平面EBD⊥平面ABCD; 分析 (1)连结BD,AC相交于点 O,连结EO,由题可知O为AC的中点,又E为PA的中点,由三角形中位线定理可得OE∥PC,得到OE⊥平面ABCD,再由面面垂直的判定可得平面EBD⊥平面ABCD;
(2)由已知结合等积法求得A到平面PBC的距离为$\sqrt{3}$,再由E为PA的中点,可得E点到平面PBC的距离;
(3)过点O作OF垂直BE于F点,连结OF,AF,由线面垂直的判定可得AO⊥平面BDE,BE⊥平面AOF,得到二面角A-EB-D的平面角为∠AFO,求解直角三角形得答案.
解答 (1)证明:连结BD,AC相交于点 O,连结EO,
∵四边形ABCD为平行四边形,∴O为AC的中点,
又∵E为PA的中点,∴OE∥PC,
由PC⊥平面ABCD,∴OE⊥平面ABCD,
又∵OE?平面EBD,∴平面EBD⊥平面ABCD;
(2)解:VA-PBC=VP-ABC,
由ABCD是菱形,且边长为2,∠ABC=60°,PC⊥平面ABCD,PC=2,
得${S}_{△ABC}=\sqrt{3}$,S△PBC=2,可得A到平面PBC的距离为$\sqrt{3}$,
∵E为PA的中点,∴E点到平面PBC的距离为$\frac{\sqrt{3}}{2}$;
(3)解:过点O作OF垂直BE于F点,连结OF,AF,
由AO⊥BD,AO⊥OE,BD∩OE=O,∴AO⊥平面BDE,
AO⊥BE,OF⊥BE,AO∩OF=O,BE⊥平面AOF.
∴二面角A-EB-D的平面角为∠AFO,
在直角△AFO中,tan∠AFO=$\frac{AO}{OC}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查面面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,考查二面角的平面角的求法,是中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 7816 | 6572 | 0802 | 6316 | 0702 | 4369 | 9728 | 1198 |
| 3204 | 9234 | 4915 | 8200 | 3623 | 4869 | 6938 | 7481 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{2}$,-$\frac{π}{4}$) | B. | (0,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com