
| A. | $\frac{4}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | 4 | D. | $\frac{{4\sqrt{6}}}{3}$ |
分析 根据双曲线和椭圆的性质和关系,结合余弦定理即可得到结论.
解答 解:设椭圆的长半轴为a,双曲线的实半轴为a1,(a>a1),半焦距为c,
由椭圆和双曲线的定义可知,
设|PF1|=r1,|PF2|=r2,|F1F2|=2c,
椭圆和双曲线的离心率分别为e1,e2
∵∠F1PF2=$\frac{π}{3}$,则由余弦定理可得4c2=(r1)2+(r2)2-2r1r2cos$\frac{π}{3}$,①
在椭圆中,①化简为即4c2=4a2-3r1r2…②,
在双曲线中,①化简为即4c2=4a12+r1r2…③,
$\frac{1}{{{e}_{1}}^{2}}$+$\frac{3}{{{e}_{2}}^{2}}$=4,
由柯西不等式得(1+$\frac{1}{3}$)($\frac{1}{{{e}_{1}}^{2}}$+$\frac{3}{{{e}_{2}}^{2}}$)=($\frac{1}{{e}_{1}}$+$\frac{\sqrt{3}}{{e}_{2}}$×$\frac{1}{\sqrt{3}}$)2
∴$\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$≤$\frac{4\sqrt{3}}{3}$
故选:B.
点评 本题主要考查椭圆和双曲线的定义和性质,利用余弦定理和柯西不等式是解决本题的关键.属于难题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
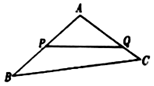 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{4}+\frac{3}{4}i$ | B. | $\frac{1}{4}-\frac{3}{4}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com