
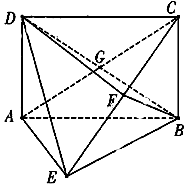
 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G.分析 (1)连接FG,推导出BF⊥CE,从而得到FG∥AE,由此能证明AE∥平面BFD.
(2)推导出BC⊥AE,BF⊥AE,AE⊥BE,以A为原点建立空间直角坐标系,利用向量法能求出直线DE与平面ACE所成的角.
解答 证明:(1)连接FG,因为BF⊥平面ACE,CE?平面ACE,所以BF⊥CE.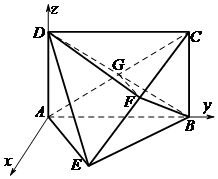
又因为EB=BC,所以F为EC的中点,
而矩形ABCD中,G为AC的中点,所以FG∥AE,
又因为AE?平面BFD,FG?平面BFD,
所以AE∥平面BFD. …(5分)
解:(2)因为DA⊥平面ABE,BC∥DA,
所以BC⊥平面ABE,所以BC⊥AE.
又因为BF⊥平面ACE,AE?平面ACE,所以BF⊥AE.
而BC∩BF=B,所以AE⊥平面BCE,所以AE⊥BE.
又因为AE=EB=2,所以$AB=2\sqrt{2}$.以A为原点建立如图所示的空间直角坐标系,
由题意得A(0,0,0),$E(\sqrt{2},\sqrt{2},0)$,D(0,0,2),$C(0,2\sqrt{2},2)$,
所以$\overrightarrow{AE}=(\sqrt{2},\sqrt{2},0)$,$\overrightarrow{AC}=(0,2\sqrt{2},2)$
设平面ACE的一个法向量为$\vec n=(x,y,z)$,
由$\left\{\begin{array}{l}\vec n•\overrightarrow{AE}=0\\ \vec n•\overrightarrow{AC}=0\end{array}\right.$,得$\left\{\begin{array}{l}\sqrt{2}x+\sqrt{2}y=0\\ 2\sqrt{2}y+2z=0\end{array}\right.$,
令x=1,得$\vec n=(1,-1,\sqrt{2})$,
又因为$\overrightarrow{DE}=(\sqrt{2},\sqrt{2},-2)$,
设直线DE与平面ACE所成的角为α,
则$sinα=|{cos<\vec n,\overrightarrow{DE}>}|=\frac{{|{\vec n•\overrightarrow{DE}}|}}{{|{\vec n}|•|{\overrightarrow{DE}}|}}=\frac{{|{\sqrt{2}-\sqrt{2}-2\sqrt{2}}|}}{{\sqrt{4}•\sqrt{8}}}=\frac{1}{2}$,所以$α=\frac{π}{6}$,
故直线DE与平面ACE所成的角为$\frac{π}{6}$. …(12分)
点评 本题考查直线与平面平行的证明,考查线面角的求法,考查空间想象能力、运算求解能力,考查数形结合思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{3}}{9}$ | C. | -$\frac{\sqrt{3}}{6}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com