
分析 (1)根据对数运算性质和对数函数的单调性得出关于x的恒等式,分离参数求出函数的最值即可得出t的范围;
(2)利用对数运算性质得出F(x)的解析式,讨论a的范围列出方程得出a的值.
解答 解:(1)∵2f(x)≥g(x)恒成立,即2logax≥loga(2x+t-2)恒成立,
∵0<a<1,∴x2≤2x+t-2恒成立,即t≥x2-2x+2恒成立,x∈[$\frac{1}{4}$,2],
令h(x)=x2-2x+2=(x-1)2+1,∴当x=2时,h(x)取得最大值2,
∴t≥2.
(2)当t=4时,F(x)=2loga(2x+2)-logax=loga$\frac{4(x+1)^{2}}{x}$=loga[4(x+$\frac{1}{x}+2$)].
令p(x)=4(x+$\frac{1}{x}+2$),则p′(x)=4(1-$\frac{1}{{x}^{2}}$),
∴当$\frac{1}{4}$≤x<1时,p′(x)<0,当1<x≤2时,p′(x)>0,
∴p(x)在[$\frac{1}{4}$,1]上单调递减,在[1,2]上单调递增.
又p($\frac{1}{4}$)=25,p(1)=16,p(2)=18,
∴p(x)在[$\frac{1}{4}$,2]上的最大值为25,最小值为16.
若a>1,则F(x)的最小值为loga16=-2,解得a=$\frac{1}{4}$(舍);
若0<a<1,则F(x)的最小值为loga25=-2,解得a=$\frac{1}{5}$.
综上:a=$\frac{1}{5}$.
点评 本题考查了对数函数的性质,函数恒成立问题,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+x+1≥0 | B. | ?x∉R,x2+x+1≥0 | ||
| C. | ?x0∉R,x02+x0+1<0 | D. | ?x0∈R,x02+x0+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
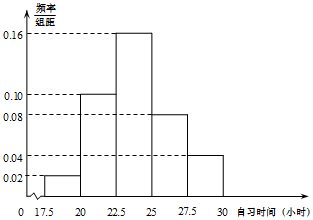 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )| A. | 30 | B. | 60 | C. | 80 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com