
分析 (1)利用立方和公式和基本不等式证明;
(2)把a+b+c=1代入$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$,再利用基本不等式得出结论.
解答 证明:(1)∵a,b,c都是正实数,
∴a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac,
以上各式相加得2a2+2b2+2c2≥2ab+2bc+2ac,
∴3a2+3b2+3c2≥a2+b2+c2+2ab+2bc+2ac=(a+b+c)2=1,
a2+b2+c2≥$\frac{1}{3}$,当且仅当a=b=c时取等号.
(2)∵a+b+c=1.
∴$\frac{b}{a}+\frac{a}{b}$≥2,$\frac{c}{a}+\frac{a}{c}$≥2,$\frac{c}{b}+\frac{b}{c}$≥2,
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$=$\frac{a+b+c}{a}$+$\frac{a+b+c}{b}$+$\frac{a+b+c}{c}$=3+$\frac{b}{a}+\frac{a}{b}$+$\frac{c}{a}+\frac{a}{c}$+$\frac{c}{b}+\frac{b}{c}$≥3+2+2+2=9.
当且仅当a=b=c时取等号.
点评 本题考查了不等式的证明,基本不等式的应用,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $-\frac{{\sqrt{6}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ③④ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-2,2) | C. | (-∞,2)∪(2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
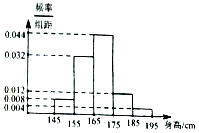 某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.
某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com