
| A. | (-∞,-2) | B. | (-2,2) | C. | (-∞,2)∪(2,+∞) | D. | (2,+∞) |
分析 求出导函数,函数的定义域x>0.利用导函数的极值与0的关系,列出不等式求解即可.
解答 解:函数f(x)=$\frac{1}{2}$x2-ax+lnx,可得f′(x)=x-a+$\frac{1}{x}$=$\frac{{x}^{2}-ax+1}{x}$,(x>0).
因为函数f(x)=$\frac{1}{2}$x2-ax+lnx有极值,所以导函数的极小值小于0,g(x)=x2-ax+1在(0,+∞)函数值有负值,
当a≤0时,必须g(0)<0不成立;当a>0时,对称轴x=$\frac{a}{2}$,满足($\frac{a}{2}$)2-a$•\frac{a}{2}$+1<0,解得a∈(2,+∞).
故选:D.
点评 本题考查了利用导数研究函数的单调性极值,考查了分类讨论的思想方法,考查了转化方法,考查了推理能力与计算能力,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$i | D. | -$\frac{3}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<3} | B. | {x|-3<x<5} | C. | {x|x<-1或x>3} | D. | {x|-1<x<5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
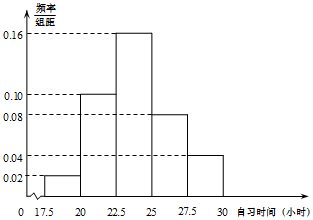 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )| A. | 30 | B. | 60 | C. | 80 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | 9 | C. | 10 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com