
分析 3次摸球所得总分至少是25分是指摸出的3个球都是红球或摸出的3个为2红1黑,由此利用n次独立重复试验中事件A恰好发生k次的概率计算公式能求出3次摸球所得总分至少是25分的概率.
解答 解:袋子中有大小、质地相同的红球、黑球各一个,现有放回地随机摸取3次,每次摸取一个球,
摸出红球,得10分,摸出黑球,得5分,
∴3次摸球所得总分至少是25分是指摸出的3个球都是红球或摸出的3个为2红1黑,
∴3次摸球所得总分至少是25分的概率是p=${C}_{3}^{3}(\frac{1}{2})^{3}+{C}_{3}^{2}(\frac{1}{2})^{2}(\frac{1}{2})$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查概率的求法,涉及到互斥事件概率计算公式、n次独立重复试验中事件A恰好发生k次的概率计算公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-2,2) | C. | (-∞,2)∪(2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 保养车辆尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
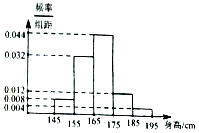 某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.
某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 23 | B. | 27 | C. | 31 | D. | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com