
分析 (1)利用组合数的计算公式可得:(k+1)${∁}_{n+1}^{k+1}$=(k+1)•$\frac{(n+1)!}{(k+1)!(n-k)!}$=$\frac{(n+1)×n!}{k!(n-k)!}$.
(2)由(1)可得:$\frac{{∁}_{n}^{k}}{k+1}$=$\frac{{∁}_{n+1}^{k+1}}{n+1}$,左边=$\sum_{k=0}^{n}\frac{(-1)^{k}}{n+1}{∁}_{n+1}^{k+1}$=$\frac{-1}{n+1}$$\sum_{k=0}^{n}{∁}_{n+1}^{k+1}$(-1)k+1=$\frac{-1}{n+1}$[(1-1)n+1-1],即可证明.
(3)$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}$${∁}_{n}^{k}$=$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}({∁}_{n-1}^{k}+{∁}_{n-1}^{k-1})$=$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n-1}^{k}$+$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n-1}^{k-1}$.由(2)可知:$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n-1}^{k-1}$=$\sum_{k=0}^{n-1}\frac{(-1)^{k}}{k+1}$${∁}_{n-1}^{k}$=$\frac{1}{n}$.设f(n)=$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n}^{k}$,则f(1)=1,$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n-1}^{k}$=f(n-1).可得f(n)-f(n-1)=$\frac{1}{n}$.利用累加求和方法即可得出.
解答 证明:(1)(k+1)${∁}_{n+1}^{k+1}$=(k+1)•$\frac{(n+1)!}{(k+1)!(n-k)!}$=$\frac{(n+1)×n!}{k!(n-k)!}$=(n+1)${∁}_{n}^{k}$.
(2)由(1)可得:$\frac{{∁}_{n}^{k}}{k+1}$=$\frac{{∁}_{n+1}^{k+1}}{n+1}$,
∴左边=$\sum_{k=0}^{n}\frac{(-1)^{k}}{n+1}{∁}_{n+1}^{k+1}$=$\frac{-1}{n+1}$$\sum_{k=0}^{n}{∁}_{n+1}^{k+1}$(-1)k+1=$\frac{-1}{n+1}$[(1-1)n+1-1]=$\frac{1}{n+1}$=右边.
∴$C_n^0-\frac{1}{2}C_n^1+\frac{1}{3}C_n^2-\frac{1}{4}C_n^3+…+\frac{{{{({-1})}^n}}}{n+1}C_n^n=\frac{1}{n+1}$.
(3)$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}$${∁}_{n}^{k}$=$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}({∁}_{n-1}^{k}+{∁}_{n-1}^{k-1})$=$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n-1}^{k}$+$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n-1}^{k-1}$
由(2)可知:$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n-1}^{k-1}$=$\sum_{k=0}^{n-1}\frac{(-1)^{k}}{k+1}$${∁}_{n-1}^{k}$=$\frac{1}{n}$.
设f(n)=$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n}^{k}$,则f(1)=1,$\sum_{k=1}^{n}\frac{(-1)^{k-1}}{k}{∁}_{n-1}^{k}$=f(n-1).
∴f(n)-f(n-1)=$\frac{1}{n}$.
∴n≥2时,f(n)=f(1)+f(2)-f(1)+…+f(n)-f(n-1)
=1+$\frac{1}{2}$+…+$\frac{1}{n}$.n=1时也成立.
∴f(n)=1+$\frac{1}{2}$+…+$\frac{1}{n}$.n∈N*.
即:$C_n^1-\frac{1}{2}C_n^2+\frac{1}{3}C_n^3-\frac{1}{4}C_n^4+…+\frac{{{{({-1})}^{n-1}}}}{n}C_n^n=1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$.
点评 本题考查了组合数计算公式、累加求和方法、转化方法,考查了推理能力与计算能力,属于难题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
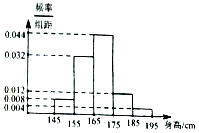 某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.
某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 7 | C. | 10 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com