
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的零点个数.
的零点个数.
(2)![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)见解析(2)见解析
【解析】
(1)求函数![]() 的导数,利用导数判断函数的单调性和极值,从而得到零点的个数;
的导数,利用导数判断函数的单调性和极值,从而得到零点的个数;
(2)![]() ,求导得
,求导得![]() ,可以判断
,可以判断![]() 存在零点
存在零点![]() ,可以求出函数
,可以求出函数![]() 的最小值为
的最小值为![]() ,可以证明出:
,可以证明出:
![]() ,
,![]() ,可证明
,可证明![]() 在
在![]() 上有零点,
上有零点,
![]() 的最小值为
的最小值为![]() ,结合
,结合![]() ,可求
,可求![]() 的最小值为
的最小值为![]() .
.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
①当![]() 时,
时,![]() ,
,![]() 单调递增,又
单调递增,又![]() ,
,![]() ,
,
所以函数![]() 有唯一零点;
有唯一零点;
②当![]() 时,
时,![]() 恒成立,所以函数
恒成立,所以函数![]() 无零点;
无零点;
③当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() .
.
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 无零点.
无零点.
综上所述,当![]() 时函数
时函数![]() 无零点.当
无零点.当![]() ,函数
,函数![]() 有一个零点.
有一个零点.
(2)由题意得,![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上为增函数,即
上为增函数,即![]() 在
在![]() 上为增函数.
上为增函数.
又![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() ,
,
且![]() ,
,![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数,当
上为减函数,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,![]() 的最小值
的最小值![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
由![]() 得
得![]() ,易知
,易知![]() 在
在![]() 上为增函数.
上为增函数.
因为![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() 在
在
![]() 上存在唯一零点
上存在唯一零点![]() ,且
,且![]() ,
,![]() ,当
,当![]() 时,
时,
![]() ,
,![]() 在
在![]() 上为减函数,当
上为减函数,当![]() 时,
时,![]() ,
,![]() 在
在![]()
上为增函数,所以![]() 的最小值为
的最小值为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
又函数![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,
,


因为![]() ,所以
,所以![]() ,即
,即![]() 在
在![]() 上的最小值为0.
上的最小值为0.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|,不等式f(x)≤4的解集为{x|-2≤x≤6}.
(1)求实数a的值;
(2)设g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下扇形统计图:

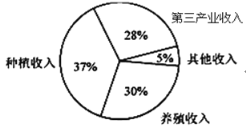
建设前经济收入构成比例建设后经济收入构成比例则下面结论中不正确的是( )
A.新农村建设后,种植收入略有增加.
B.新农村建设后,其他收入增加了一倍以上.
C.新农村建设后,养殖收入不变.
D.新农村建设后,种植收入在经济收入中所占比重大幅下降.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十八届五中全会首次提出了绿色发展理念,将绿色发展作为“十三五”乃至更长时期经济社会发展的一个重要理念.某地区践行“绿水青山就是金山银山”的绿色发展理念,2015年初至2019年初,该地区绿化面积y(单位:平方公里)的数据如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
绿化面积y | 2.8 | 3.5 | 4.3 | 4.7 | 5.2 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)利用(1)中的回归方程,预测该地区2025年初的绿化面积.
(参考公式:线性回归方程:![]() ,
,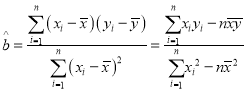 ,
,![]() 为数据平均数)
为数据平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在抛物线![]() 上,且点P的横坐标为2,以P为圆心,
上,且点P的横坐标为2,以P为圆心,![]() 为半径的圆(O为原点),与抛物线C的准线交于M,N两点,且
为半径的圆(O为原点),与抛物线C的准线交于M,N两点,且![]() .
.
(1)求抛物线C的方程;
(2)若抛物线的准线与y轴的交点为H.过抛物线焦点F的直线l与抛物线C交于A,B,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为确定下一年投入某种产品的研发费用,需了解年研发费用![]() (单位:千万元)对年销售量
(单位:千万元)对年销售量![]() (单位:千万件)的影响,统计了近
(单位:千万件)的影响,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 与年销售量
与年销售量![]() 的数据,得到散点图如图所示:
的数据,得到散点图如图所示:
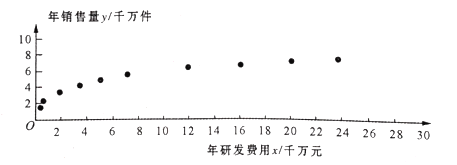
(Ⅰ)利用散点图判断,![]() 和
和![]() (其中
(其中![]() ,
,![]() 为大于
为大于![]() 的常数)哪一个更适合作为年研发费用
的常数)哪一个更适合作为年研发费用![]() 和年销售量
和年销售量![]() 的回归方程类型(只要给出判断即可,不必说明理由);
的回归方程类型(只要给出判断即可,不必说明理由);
(Ⅱ)对数据作出如下处理:令![]() ,
,![]() ,得到相关统计量的值如下表:
,得到相关统计量的值如下表:

根据(Ⅰ)的判断结果及表中数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)已知企业年利润![]() (单位:千万元)与
(单位:千万元)与![]() ,
,![]() 的关系为
的关系为![]() (其中
(其中![]() ),根据(Ⅱ)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
),根据(Ⅱ)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为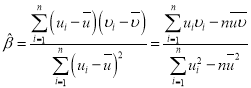 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,直线
,直线![]() ,动直线
,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)以曲线![]() 上的点
上的点![]() 为切点做曲线
为切点做曲线![]() 的切线
的切线![]() ,设
,设![]() 分别与
分别与![]() 、
、![]() 轴交于
轴交于![]() 两点,且
两点,且![]() 恰与以定点
恰与以定点![]() 为圆心的圆相切.当圆
为圆心的圆相切.当圆![]() 的面积最小时,求
的面积最小时,求![]() 与
与![]() 面积的比.
面积的比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月6日北京时间上午11时30分,朝鲜中央电视台宣布“成功进行了氢弹试验”,再次震动世界,此事件也引起了我国公民热议,其中丹东市(丹东市和朝鲜隔江)某QQ聊天群有300名网友,乌鲁木齐市某微信群有200名网友,为了解不同地区我国公民对“氢弹试验”事件的关注程度,现采用分层抽样的方法,从中抽取了100名网友,先分别统计了他们在某时段发表的信息条数,再将两地网友发表的信息条数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.
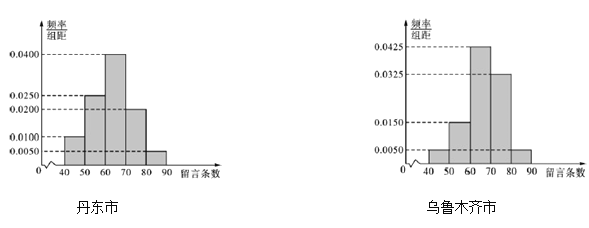
(1)求丹东市网友的平均留言条数(保留整数);
(2)为了进一步开展调查,从样本中留言条数超过80条的网友中随机抽取2人,求至少抽到一名乌鲁木齐市网友的概率;
(3)规定“留言条数”不少于70条为“强烈关注”.
①请你根据已知条件完成下列2×2的列联表:
强烈关注 | 非强烈关注 | 合计 | |
丹东市 | |||
乌鲁木齐市 | |||
合计 |
②判断是否有90%的把握认为“强烈关注”与网友所在的地区有关?
附:临界值表及参考公式:
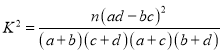 ,
,![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com