
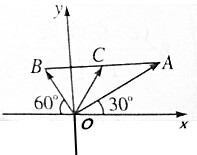
分析 根据题意,结合图形,写出$\overrightarrow{OA}$、$\overrightarrow{OB}$的坐标表示,再求$\overrightarrow{OC}$的坐标表示即可.
解答 解:根据题意,结合图形,得
$\overrightarrow{OA}$=(2cos30°,2sin30°)=($\sqrt{3}$,1),
$\overrightarrow{OB}$=(-cos60°,sin60°)=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
∴$\overrightarrow{OC}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\frac{1}{2}$($\sqrt{3}$-$\frac{1}{2}$,1+$\frac{\sqrt{3}}{2}$)=($\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$).
故答案为:($\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$).
点评 本题考查了平面向量的坐标运算与应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com