考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)运用椭圆的离心率公式,点在椭圆上,及a,b,c的关系,解方程,即可得到椭圆方程;
(2)设出直线PA的方程,联立椭圆方程,消去y,再由相切的条件,得到判别式为0,化简整理,结合A在椭圆上,即可得到直线PA的方程,进而得到直线PB的方程,求出直线AB的斜率,求出AB的方程,即可得到恒过定点.
解答:
(1)解:由于椭圆的离心率为
,即有e=
=
,①
点D(
,
)在该椭圆上,则有
+
=1,
解得,b=1,则a
2-c
2=1,②
由①②解得,a=2,c=
.
则椭圆方程为:
+y
2=1;
(2)证明:设直线PA:y-y
1=k(x-x
1),
联立椭圆方程x
2+4y
2=4,
消去y,可得,(1+4k
2)x
2+8k(y
1-kx
1)x+4(y
1-kx
1)
2-4=0,
由于相切,则有判别式△=64k
2(y
1-kx
1)
2-16(1+4k
2)[(y
1-kx
1)
2-1]=0,
化简得,(y
1-kx
1)
2-1-4k
2=0,
由于A在椭圆上,则x
12+4y
12=4,即有x
12-4=-4y
12,y
12-1=-
x
12,
则有(y
12-1)+k
2(x
12-4)-2kx
1y
1=0,
即有-
x
12-4k
2y
12-2kx
1y
1=0,即(
+2ky
1)
2=0,
则k=
,代入直线PA的方程,则有y-y
1=
(x-x
1),
整理,即得
+y
1y=
+y
12=1,
则直线PA方程为
+yy
1=1.
同理可得直线PB的方程为
+y
2y=1,
设P(
,n),则有
x
1+ny
1=1,
x
2+ny
2=1,
两式相减可得,
(x
1-x
2)+n(y
1-y
2)=0,
则有AB的斜率为:k
AB=
=-
,
则直线AB:y-y
1=-
(x-x
1),
即有ny-ny
1=ny-(1-
x
1)=-
x+
x
1,
即有ny=1-
x,由
解得,
.
则有恒过定点(
,0),
点评:本题考查椭圆的方程和性质,考查直线方程和椭圆方程联立,消去未知数,运用判别式为0,考查直线的斜率公式,直线恒过定点问题,考查化简整理运算能力,属于中档题.



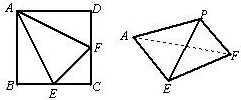 正方形ABCD的边长为1,E、F分别为BC、CD的中点,沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P,则P到面AEF的距离为
正方形ABCD的边长为1,E、F分别为BC、CD的中点,沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P,则P到面AEF的距离为