练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．90×91×92×…×100=（　　）
    A．A${\;}_{100}^{10}$B．A${\;}_{100}^{11}$C．A${\;}_{100}^{12}$D．A${\;}_{101}^{11}$

    分析 根据排列数的公式${A}_{n}^{m}$=n（n-1）（n-2）…（n-m+1），写出结果即可．

    解答 解：根据排列数的公式，得；
    90×91×92×…×100=${A}_{100}^{100-90+1}$=${A}_{100}^{11}$．
    故选：B．

    点评 本题考查了排列数公式的逆用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．某校对高一年级学生的数学成绩进行统计，全年级同学的成绩全部介于60分与100分之间，将他们的成绩数据绘制成如图所示的频率分布直方图．现从全体学生中，采用分层抽样的方法抽取60名同学的试卷进行分析，则从成绩在[90，100]内的学生中抽取的人数为（　　）
    A．24B．18C．15D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．同时投掷两颗骰子，则两颗骰子向上的点数相同的概率为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{6}$D．$\frac{1}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知等差数列{an}的前n项和为Sn，若$\overrightarrow{OB}$=a1 $\overrightarrow{OA}$+a2011$\overrightarrow{OC}$，且A、B、C三点共线（O为该直线外一点），则S2011=（　　）
    A．2011B．$\frac{2011}{2}$C．22011D．2-2011

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知△ABC的内角A、B、C所对的边分别为a，b，c，且cosB=$\frac{4}{5}$，b=2．
    （Ⅰ）当a=$\frac{5}{3}$时，求A；
    （Ⅱ）当a+c=2$\sqrt{10}$时，求△ABC的面积S．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在△ABC中，已知$\overrightarrow{AB}•\overrightarrow{AC}$=2$\sqrt{3}$，A=60°，则△ABC的面积为（　　）
    A．1B．2C．$\frac{3}{2}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

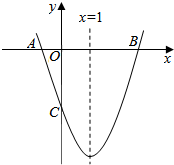    19．如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．
    （1）求这条抛物线所对应的函数关系式；
    （2）在抛物线的对称轴x=1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标；
    （3）设点P为抛物线的对称轴x=1上的一动点，求使∠PCB=90°的点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源：2017届广西陆川县中学高三9月月考数学（文）试卷（解析版） 题型：填空题

    已知是上的奇函数，且时，，则的值为____________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图，已知圆O：x2+y2=4与轴正半轴交于点P，A（-1，0），B（1，0），直线l与圆O切于点S（l不垂直于x轴），抛物线过两点A，B且以l为准线．
     （1）当点S在圆周上运动时，求证：抛物线的焦点Q始终在某一椭圆C上，并求出该椭圆C的方程；
    （2）设M．N是（1）中椭圆C上除短轴端点外的不同两点，且$\overrightarrow{PM}$=t$\overrightarrow{PN}$（t∈R），问：△MON的面积是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案