Question

13．中国传统文化中很多内容体现了数学的对称美，如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的形式美、和谐美，给出定义：能够将圆B的周长和面积同时平分的函数称为这个圆的“优美函数”，给出下列命题：
①对于任意一个圆B，其“优美函数”有无数个；
②函数f（x）=ln（x²+$\sqrt{{x}^{2}+1}$可以是某个圆的“优美函数”；
③正弦函数y=sinx可以同时是无数个圆的“优美函数”；
④函数y=f（x）是“优美函数”的充要条件为函数y=f（x）的图象是中心对称图形．
其中正确的命题是（　　）

• A． ①③
• B． ①③④
• C． ②③
• D． ①④

Answer 1

分析 ①过圆心的直线都可以将圆的周长和面积同时平分；
②作函数f（x）的大致图象，即可判断命题的正误；
③将圆的圆心放在正弦函数y=sinx的对称中心上，
即可得出正弦函数y=sinx是该圆的“优美函数”；
④函数y=f（x）的图象是中心对称图形，y=f（x）是“优美函数”，
函数y=f（x）是“优美函数”时，图象不一定是中心对称图形．

解答 解：对于①，过圆心的直线都可以将圆的周长和面积同时平分，
故对于任意一个圆O，其“优美函数”有无数个，①正确；
对于②，函数f（x）=ln（x²+$\sqrt{{x}^{2}+1}$）为定义域R上的偶函数，其大致图象如图1，
∴f（x）不可能为圆的“优美函数”，②错误；
对于③，将圆的圆心放在正弦函数y=sinx的对称中心上，
则正弦函数y=sinx是该圆的“优美函数”，
∴有无数个圆成立，③正确；
对于④，函数y=f（x）的图象是中心对称图形，则y=f（x）是“优美函数”，
但函数y=f（x）是“优美函数”时，图象不一定是中心对称图形，
如图2所示，④错误；
正确的命题序号是①③．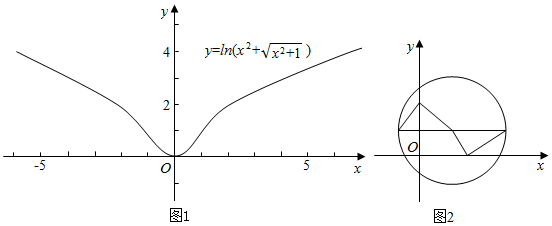

故选：A．

点评 本题考查了命题真假的判断问题，也考查了函数性质以及新定义的应用，是综合题．