
已知函数f(x)=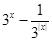 .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若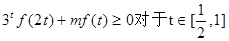 恒成立,求m的取值范围。
恒成立,求m的取值范围。
(1) x=log3(1+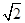 ) ;
) ;
(2) f(x)=3x-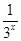 在(0,+∞)上单调递增 ;
在(0,+∞)上单调递增 ;
(3) [-4,+∞).
解析试题分析:(1)当x≤0时,f(x)=3x-3x=0,∴f(x)=2无解.
当x>0时,f(x)=3x-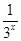 ,令3x-
,令3x-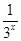 =2,
=2,
∴(3x)2-2·3x-1=0,∴3x=1±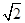 .
.
∵3x>0,∴3x=1-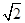 (舍).∴3x=1+
(舍).∴3x=1+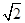 .∴x=log3(1+
.∴x=log3(1+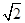 ) 4分
) 4分
(2)当x>0,f(x)=3x-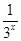 .∵y=3x在(0,+∞)上单调递增,
.∵y=3x在(0,+∞)上单调递增,
y=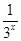 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.
∴f(x)=3x-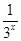 在(0,+∞)上单调递增 8分
在(0,+∞)上单调递增 8分
(3)∵t∈[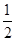 ,1],∴f(t)=3t-
,1],∴f(t)=3t-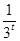 >0,
>0,
∴3tf(2t)+mf(t)≥0化为3t(32t-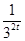 )+m(3t-
)+m(3t-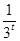 )≥0.
)≥0.
即3t(3t+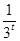 )+m≥0.即m≥-32t-1.
)+m≥0.即m≥-32t-1.
令g(t)=-32t-1,则g(t)在[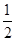 ,1]上递减,
,1]上递减,
∴g(x)max=-4.
∴所求实数m的取值范围是[-4,+∞) 13分
考点:本题主要考查指数函数的性质,指数方程的解法,不等式恒成立问题。
点评:中档题,解简单的指数方程,一般是考虑化同底数指数幂相等或利用“换元法”,转化成一元二次方程求解。不等式恒成立问题,一般是利用“分离参数法”,转化成求函数最值问题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)= ,g(x)=2|x|+a.
,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若存在x∈ R,使得f(x)≥g(x)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知指数函数 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为 的函数
的函数 是奇函数。
是奇函数。
(1)确定 的解析式;(2)求m,n的值;
的解析式;(2)求m,n的值;
(3)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com