
| A. | 6 | B. | 9 | C. | 3 | D. | 2 |
分析 化圆的一般式方程为标准式,求出圆心坐标,得到D、E的值,则半径可求.
解答 解:由x2+y2+Dx+Ey-4=0,得$(x+\frac{D}{2})^{2}+(y+\frac{E}{2})^{2}=\frac{{D}^{2}}{4}+\frac{{E}^{2}}{4}+4$,
∴圆心坐标为(-$\frac{D}{2}$,-$\frac{E}{2}$),
则$\left\{\begin{array}{l}{-\frac{D}{2}=-1}\\{-\frac{E}{2}=2}\end{array}\right.$,即D=2,E=-4.
∴圆的半径r=$\sqrt{\frac{{2}^{2}}{4}+\frac{(-4)^{2}}{4}+4}=3$.
故选:C.
点评 本题考查圆的一般式方程,考查了一般式化标准式,是基础题.


科目:高中数学 来源: 题型:选择题
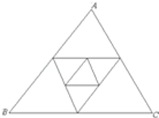 如图,已知△ABC周长为2,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为( )
如图,已知△ABC周长为2,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为( )| A. | $\frac{1}{2002}$ | B. | $\frac{1}{2001}$ | C. | $\frac{1}{{2}^{2002}}$ | D. | 2${\;}^{\frac{1}{2001}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48.
如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
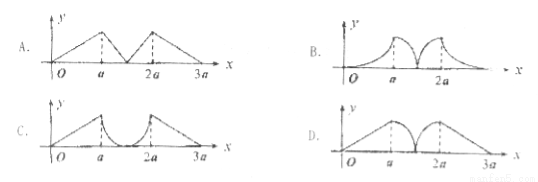
如图所示,点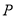 从点
从点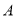 处出发,按逆时针方向沿边长为
处出发,按逆时针方向沿边长为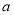 的正三角形
的正三角形 运动一周,
运动一周,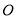 为
为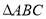 的中心,设点
的中心,设点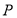 走过的路程为
走过的路程为 ,
,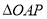 的面积为
的面积为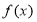 (当
(当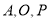 三点共线时,记面积为0),则函数
三点共线时,记面积为0),则函数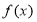 的图象大致为( )
的图象大致为( )
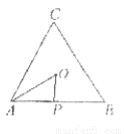
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com