
分析 (Ⅰ)利用奇函数的定义,即可证明结论;
(Ⅱ)不妨设a≤b,则M=b,x-A>0,方程f(x)=$\frac{λ}{x-A}$+A等价于[x-A+$\frac{2(x-A)}{(x-a)(x-b)}$](x-A)=λ.令$\frac{b-a}{2}$=d,t=(x-A)2>$(\frac{b-a}{2})^{2}$=d2>0,则$\frac{{t}^{2}+(2-{d}^{2})t}{t-{d}^{2}}$=λ.令u=t-d2,则λ=u+$\frac{2{d}^{2}}{u}$+2+d2≥2$\sqrt{2}$d+2+d2=$(\frac{b-a}{2}+\sqrt{2})^{2}$,即可得出结论.
解答 解:(Ⅰ)易知函数定义域关于原点对称.
∵a+b=0,∴$f(x)=x+\frac{1}{x-a}+\frac{1}{x+a}$$f(-x)=-x+\frac{1}{-x-a}+\frac{1}{-x+a}=-f(x)$
∴f(x)为奇函数; …(5分)
(Ⅱ)不妨设a≤b,则M=b,x-A>0,方程f(x)=$\frac{λ}{x-A}$+A等价于[x-A+$\frac{2(x-A)}{(x-a)(x-b)}$](x-A)=λ.
令$\frac{b-a}{2}$=d,则x-a=(x-A)=d,x-b=(x-A)+d,
∴(x-A)2[1+$\frac{2}{[(x-A)-d]•[(x-A)+d]}$=λ,
令t=(x-A)2>$(\frac{b-a}{2})^{2}$=d2>0,则$\frac{{t}^{2}+(2-{d}^{2})t}{t-{d}^{2}}$=λ.
令u=t-d2,则λ=u+$\frac{2{d}^{2}}{u}$+2+d2≥2$\sqrt{2}$d+2+d2=$(\frac{b-a}{2}+\sqrt{2})^{2}$,
当且仅当u=$\frac{2{d}^{2}}{u}$,即t=$\sqrt{2}d+{d}^{2}$,x=$\frac{b+a}{2}+\frac{\sqrt{(b-a)^{2}+2\sqrt{2}(b-a)}}{2}$∈(b,+∞)时取等号,
∵方程f(x)=$\frac{λ}{x-A}$+A在区间(M,+∞)上无解,
∴λ<$(\frac{b-a}{2}+\sqrt{2})^{2}$.
点评 本题考查奇函数的定义,考查方程f(x)=$\frac{λ}{x-A}$+A在区间(M,+∞)上无解,考查学生转化问题的能力,难度大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )| A. | 1:3 | B. | 3:1 | C. | 1:2 | D. | 2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
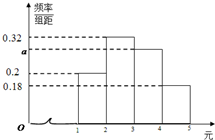 甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发50个红包,每个红包金额为x元,x∈[1,5].已知在每轮游戏中所产生的50个红包金额的频率分布直方图如图所示.
甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发50个红包,每个红包金额为x元,x∈[1,5].已知在每轮游戏中所产生的50个红包金额的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
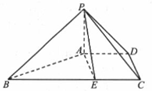 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE=$\frac{2}{3}$BC,PB⊥AE.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE=$\frac{2}{3}$BC,PB⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数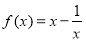 .
.
(1)用函数单调性的定义证明:函数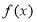 在区间
在区间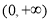 上为增函数;
上为增函数;
(2)若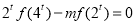 ,当
,当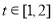 时,求实数
时,求实数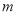 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:解答题
如图,在三棱柱 中,
中, 平面
平面 ,
,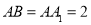 ,
, ,
, ,
,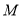 ,
, 分别为
分别为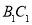 、
、 的中点.
的中点.

(1)求证:平面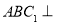 平面
平面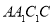 ;
;
(2)求证: 平面
平面 ,并求
,并求 到平面
到平面 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com