
 ��ͼ����֪����P-ABCD�У�����ABCD��ֱ�����Σ���ADC=90�㣬AB��CD��AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$��ƽ��PBC��ƽ��ABCD��
��ͼ����֪����P-ABCD�У�����ABCD��ֱ�����Σ���ADC=90�㣬AB��CD��AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$��ƽ��PBC��ƽ��ABCD������ ��1��ȡAB���е�E������CE���Ƶ����ı���AECD�������Σ��Ӷ�CE��AB�������AC��CB���ɴ���֤��AC��PB��
��2����BC���е�ΪF������PF���ֱ���FE��FB��FP���ڵ�ֱ��Ϊx�ᣬy�ᣬz�ᣬ�����ռ�ֱ������ϵ����������������������
��� ֤������1��ȡAB���е�E������CE��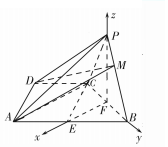
��AB��CD��DC=$\frac{1}{2}$AB����DC$\underset{��}{=}$AE��
���ı���AECD��ƽ���ı��Σ�
�֡ߡ�ADC=90�㣬���ı���AECD�������Σ���CE��AB��
���CAB�ǵ������ǿ��У���CA=CB=2��AB=2$\sqrt{2}$��
��AC2+CB2=AB2����AC��CB��
�֡�ƽ��PBC��ƽ��ABCD��ƽ��PBC��ƽ��ABCD=BC��
��AC��ƽ��PBC��
��PB?ƽ��PBC����AC��PB��
�⣺��2����BC���е�ΪF������PF��
��PB=PC����PF=BC��
��PF��ƽ��ABCD����PF��AC��
����EF����EF��AC����PF��FE��EF��BC��
�ֱ���FE��FB��FP���ڵ�ֱ��Ϊx�ᣬy�ᣬz�ᣬ�����ռ�ֱ������ϵ��
��AD=PB=PC=$\sqrt{2}$����F��0��0��0����A��2��-1��0����
B��0��1��0����D��1��-2��0����P��0��0��1����
��$\overrightarrow{PB}$=��0��1��-1����$\overrightarrow{AD}$=��-1��-1��0����$\overrightarrow{FP}$=��0��0��1����
�����߶�PB�ϴ���һ��M����$\overrightarrow{PM}$=$��\overrightarrow{PB}$����0�ܦˣ�1����
��$\overrightarrow{PM}=\overrightarrow{FM}-\overrightarrow{FP}$����$\overrightarrow{FM}=��\overrightarrow{PB}+\overrightarrow{FP}$=�ˣ�0��1��-1��+��0��0��1��=��0���ˣ�1-�ˣ���
��M��0���ˣ�1-�ˣ���$\overrightarrow{MD}=��1��-2-�ˣ�-1+�ˣ�$��
��ƽ��MAD��һ��������$\overrightarrow{m}$=��x��y��z����
��$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=x+y=0}\\{\overrightarrow{m}•\overrightarrow{MD}=x-��2+�ˣ�y-��1-�ˣ�z=0}\end{array}\right.$��ȡx=1����$\overrightarrow{m}$=��1��-1��$\frac{3+��}{1-��}$����
ƽ��ABCD�ķ�����$\overrightarrow{n}$=��0��0��1����
�߶����M-AD-B������ֵΪ$\frac{{5\sqrt{3}}}{9}$��
��|cos��$\overrightarrow{m}��\overrightarrow{n}$��|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{|\frac{3+��}{1-��}|}{\sqrt{1+1+��\frac{3+��}{1-��}��^{2}}}$=$\frac{5\sqrt{3}}{9}$��
���$��=\frac{1}{3}$���=2���ᣩ��
����ڵ�M��ʹ�ö����M-AD-B������ֵΪ$\frac{5\sqrt{3}}{9}$����$\frac{PM}{PB}$=$\frac{1}{3}$��
���� ���⿼������ֱ�ߴ�ֱ��֤�����������������ĵ��λ�õ�ȷ�������е��⣬����ʱҪ�������⣬ע���������ĺ������ã�


 �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ԭʼ���ʱ�ڣ�����ͨ���������ϴ��������������������������������ʱ��λ���ף�Ϊ��ȷ��¼���ӵijɳ��������ڴ�ϸ��ͬ�������ϴ�ᣬ��ϸ���֣����߽�һ����ͼ��ʾ�������Ѿ�����468�죮
ԭʼ���ʱ�ڣ�����ͨ���������ϴ��������������������������������ʱ��λ���ף�Ϊ��ȷ��¼���ӵijɳ��������ڴ�ϸ��ͬ�������ϴ�ᣬ��ϸ���֣����߽�һ����ͼ��ʾ�������Ѿ�����468�죮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
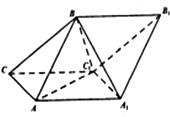 ��ͼ��б������ABC-A1B1C1�IJ���AA1C1C�����Σ�����ABB1A1�Ͳ���AA1C1C��A1B=AB=AA1=2����AA1C1�����Ϊ$\sqrt{3}$���ҡ�AA1C1Ϊ��ǣ�
��ͼ��б������ABC-A1B1C1�IJ���AA1C1C�����Σ�����ABB1A1�Ͳ���AA1C1C��A1B=AB=AA1=2����AA1C1�����Ϊ$\sqrt{3}$���ҡ�AA1C1Ϊ��ǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�찲�պϷ�һ�и�����ѧ���¿�һ��ѧ���ģ��Ծ��������棩 ���ͣ������
����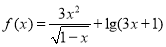 �Ķ������� .
�Ķ������� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�������ѧ�߶����¿�һ��ѧ���ģ��Ծ��������棩 ���ͣ������
������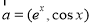 ��
��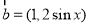 ������
������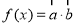 ������
������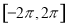 �ϵ�������Ϊ ��
�ϵ�������Ϊ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com