
分析 $\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$=$\frac{1}{3-1}+\frac{1}{{3}^{2}-1}$+$…+\frac{1}{{3}^{n}-1}$>$\frac{1}{3}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{n}}$,$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$=$\frac{1}{3-1}+\frac{1}{{3}^{2}-1}$+$…+\frac{1}{{3}^{n}-1}$<$\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n}}$,由此利用等比数列的前n项和公式能证明$\frac{1}{2}$[1-($\frac{1}{3}$)n]<$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$<1.
解答 证明:∵an=3n,
∴$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$=$\frac{1}{3-1}+\frac{1}{{3}^{2}-1}$+$…+\frac{1}{{3}^{n}-1}$
>$\frac{1}{3}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{n}}$=$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$=$\frac{1}{2}$[1-($\frac{1}{3}$)n].
$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$=$\frac{1}{3-1}+\frac{1}{{3}^{2}-1}$+$…+\frac{1}{{3}^{n}-1}$
<$\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=1-$\frac{1}{{2}^{n}}$<1.
∴$\frac{1}{2}$[1-($\frac{1}{3}$)n]<$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$<1.
点评 本题考查不等式的证明,是中档题,解题时要认真审题,注意放缩法的合理运用.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
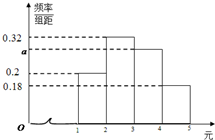 甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发50个红包,每个红包金额为x元,x∈[1,5].已知在每轮游戏中所产生的50个红包金额的频率分布直方图如图所示.
甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发50个红包,每个红包金额为x元,x∈[1,5].已知在每轮游戏中所产生的50个红包金额的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数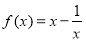 .
.
(1)用函数单调性的定义证明:函数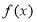 在区间
在区间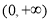 上为增函数;
上为增函数;
(2)若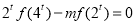 ,当
,当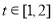 时,求实数
时,求实数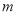 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:选择题
下列结论判断正确的是( )
A.任意两条直线确定一个平面
B.三条平行直线最多确定三个平面
C.棱长为1的正方体的内切球的表面积为
D.若平面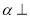 平面
平面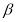 ,平面
,平面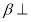 平面
平面 ,则平面
,则平面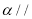 平面
平面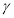
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com