
分析 (1)设幂函数f(x)=xα,利用图象过点(3,$\frac{1}{9}$)求出α的值,即得解析式;
(2)函数f(x)在(0,+∞)上是单调减函数,利用单调性定义即可证明.
解答 解:(1)设幂函数f(x)=xα,其图象过点(3,$\frac{1}{9}$),
∴3α=$\frac{1}{9}$,
解得α=-2,
∴f(x)=x-2;
(2)函数f(x)=x-2=$\frac{1}{{x}^{2}}$,在(0,+∞)上是单调减函数;
证明如下:任取x1,x2∈(0,+∞),且x1<x2,
∴f(x1)-f(x2)=$\frac{1}{{{x}_{1}}^{2}}$-$\frac{1}{{{x}_{2}}^{2}}$=$\frac{{(x}_{2}{-x}_{1}){(x}_{1}{+x}_{2})}{{{{{x}_{1}}^{2}x}_{2}}^{2}}$>0,
f(x1)>f(x2),
∴函数f(x)在(0,+∞)上的是单调减函数.
点评 本题考查了幂函数的定义与性质的应用问题,也考查了函数的单调性证明问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| y1 | y2 | 总计 | |
| x1 | * | 16 | 40 |
| x2 | a | b | * |
| 总计 | 28 | * | 70 |
| A. | 14,16 | B. | 4,26 | C. | 4,24 | D. | 26,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
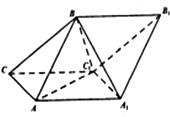 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数 .
.
(1)若函数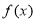 在
在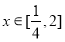 内单调递减,求实数
内单调递减,求实数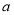 的取值范围;
的取值范围;
(2)当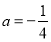 时,关于
时,关于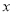 的方程
的方程 在
在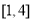 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数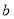 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(理)试卷(解析版) 题型:解答题
已知函数 在
在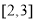 上有最小值1和最大值4,设
上有最小值1和最大值4,设 .
.
(1)求 的值;
的值;
(2)若不等式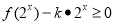 在
在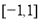 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:解答题
如图,在三棱柱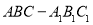 中,
中,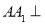 平面
平面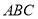 ,
, ,
,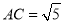 ,
,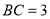 ,
,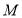 ,
,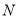 分别为
分别为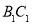 、
、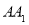 的中点.
的中点.
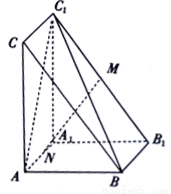
(1)求证:平面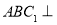 平面
平面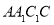 ;
;
(2)求证: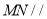 平面
平面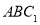 ,并求
,并求 到平面
到平面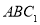 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com