
分析 先将关于x的方程ax=x,再画出a>1时函数y=ax,y=a的图象,根据图象求解函数的导数求出最小值大于0,利用对数运算法则化简求解即可.
解答 解:据题意,关于x的方程ax=x无实根.
函数y=ax,的图象与直线y=x没有的交点.
a>1时:如图: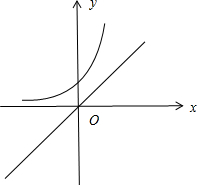
方程ax=x,即ax-x=0,令y=ax-x
函数y′=axlna-1,函数的极值点为:x=$lo{g}_{a}ln{a}^{-1}$,并且是最小值点,必须${a}^{lo{g}_{a}ln{a}^{-1}}-lo{g}_{a}ln{a}^{-1}>0$,可得:$ln{a}^{-1}>\frac{lnln{a}^{-1}}{lna}$,即1>lnlna-1,任意x使得lna-1<e,a-1<ee,∴a>${e}^{\frac{1}{e}}$.
则实数a的取值范围为 (${e}^{\frac{1}{e}}$,+∞)
故答案为:$({e^{\frac{1}{e}}},+∞)$.
点评 本题主要考查函数的导数的应用,函数的最值以及极值的求法,对数的运算法则的应用,考查数形结合,转化思想的应用,考查计算能力.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,2] | C. | [4,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
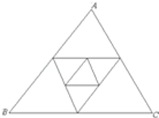 如图,已知△ABC周长为2,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为( )
如图,已知△ABC周长为2,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为( )| A. | $\frac{1}{2002}$ | B. | $\frac{1}{2001}$ | C. | $\frac{1}{{2}^{2002}}$ | D. | 2${\;}^{\frac{1}{2001}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
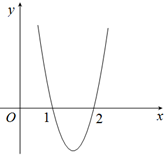 已知函数f(x)=2x3+bx2+cx,其导函数y=f′(x)的图象(如图所示)经过点(1,0),(2,0).
已知函数f(x)=2x3+bx2+cx,其导函数y=f′(x)的图象(如图所示)经过点(1,0),(2,0).查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,如图所示,孩子已经出生468天.
原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,如图所示,孩子已经出生468天.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
如图所示,点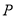 从点
从点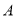 处出发,按逆时针方向沿边长为
处出发,按逆时针方向沿边长为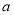 的正三角形
的正三角形 运动一周,
运动一周,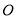 为
为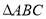 的中心,设点
的中心,设点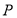 走过的路程为
走过的路程为 ,
,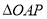 的面积为
的面积为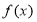 (当
(当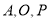 三点共线时,记面积为0),则函数
三点共线时,记面积为0),则函数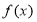 的图象大致为( )
的图象大致为( )
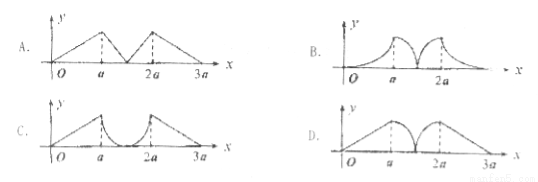
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com