
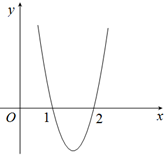
 已知函数f(x)=2x3+bx2+cx,其导函数y=f′(x)的图象(如图所示)经过点(1,0),(2,0).
已知函数f(x)=2x3+bx2+cx,其导函数y=f′(x)的图象(如图所示)经过点(1,0),(2,0).分析 (Ⅰ)根据图象可得得f'(x)=6x2+2bx+c=0的解为x=1,x=2,根据根与系数的关系,联立方程组求解即可;
(Ⅱ)根据导数求出函数的单调区间,求出相应函数值,即可求实数m的值.
解答 解:(Ⅰ)依题意,可得f'(x)=6x2+2bx+c=0的解为x=1,x=2,
故$\left\{\begin{array}{l}1+2=-\frac{b}{3}\\ 1×2=\frac{c}{6}.\end{array}\right.$解得$\left\{\begin{array}{l}b=-9\\ c=12.\end{array}\right.$
所以f(x)=2x3-9x2+12x.
(Ⅱ)f'(x)=6x2-18x+12=6(x-1)(x-2),
当f'(x)>0时,x<1或x>2;
当f'(x)<0时,1<x<2.
所以函数f(x)的单调增区间为(-∞,1)和(2,+∞),单调减区间为(1,2),
当x=1时,f(x)极大=5,当x=2时,f(x)极小=4.
故方程f(x)-m=0恰有2个根,得m=4或m=5.
点评 本题主要考查了利用导数研究函数的极值、单调性,以及观察图形的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [ln3,$\frac{3}{e}$) | C. | [ln3,$\frac{1}{e}$) | D. | (0,$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )| A. | 1:3 | B. | 3:1 | C. | 1:2 | D. | 2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
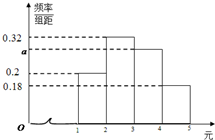 甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发50个红包,每个红包金额为x元,x∈[1,5].已知在每轮游戏中所产生的50个红包金额的频率分布直方图如图所示.
甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发50个红包,每个红包金额为x元,x∈[1,5].已知在每轮游戏中所产生的50个红包金额的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数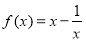 .
.
(1)用函数单调性的定义证明:函数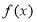 在区间
在区间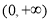 上为增函数;
上为增函数;
(2)若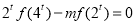 ,当
,当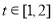 时,求实数
时,求实数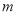 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com