练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．若由一个2×2列联表中的数据计算得有99.9%的把握认为两个变量有关系．那么K2的取值范围为K2≥10.828．（根据参照表）

    分析 根据观测值表，结合独立性检验的意义，即可得出正确的结论．

    解答 解：根据观测值表：

    P（k2≥k0）0.050.0250.0100.0050.001
    k03.8415.0246.6357.87910.828
    得，列联表中的数据计算得有99.9%的把握认为两个变量有关系．
    那么K2的取值范围是K2≥10.828．
    故答案为：K2≥10.828．

    点评 本题考查了独立性检验的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．在一次独立性检验中，得出2×2列联表如表，且最后发现两个分类变量A和B没有任何关系，则a的可能值是（　　）
    A$\overline A$合计
    B3090120
    $\overline B$24a24+a
    合计5490+a144+a
    A．72B．30C．24D．20

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知f（x）=$\frac{2}{3}$x3-2ax2-3x（a∈R）．
    （Ⅰ）若f（x）在区间（-1，1）内为减函数，求实数a的取值范围；
    （Ⅱ）对于实数a的不同取值，试讨论y=f（x）在（-1，1）内的极值点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．下面是一个2×2列联表
    y1y2总计
    x1*1640
    x2ab*
    总计28*70
    则表中a、b处的值分别为（　　）
    A．14，16B．4，26C．4，24D．26，4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

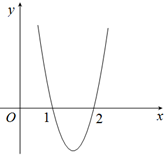    16．已知函数f（x）=2x3+bx2+cx，其导函数y=f′（x）的图象（如图所示）经过点（1，0），（2，0）．
    （Ⅰ）求f（x）的解析式；
    （Ⅱ）若方程f（x）-m=0恰有2个根，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1，过右焦点F的直线l与椭圆C交于A，B两点，当直线l的斜率为1时，坐标原点O到直线l的距离为$\frac{\sqrt{2}}{2}$．
    （1）求椭圆的离心率；
    （2）若直线可以绕点F转动，动点P在椭圆上，当$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$时，求四边形OAPB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．原始社会时期，人们通过在绳子上打结来计算数量，即“结绳计数”，当时有位父亲，为了准确记录孩子的成长天数，在粗细不同的绳子上打结，由细到粗，满七进一，如图所示，孩子已经出生468天．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在△ABC中，角A，B，C的对边分别为a，b，c，$\frac{2a+b}{cosB}$=$\frac{-c}{cosC}$．
    （1）求角C的大小；
    （2）求sinAsinB的最大值．

    查看答案和解析>>

    科目：高中数学 来源：2017届安徽合肥一中高三上学期月考一数学（文）试卷（解析版） 题型：填空题

    函数的定义域是 .

    查看答案和解析>>

    同步练习册答案