
分析 (1)F(c,0),直线l的方程为:y=x-c,可得:$\frac{c}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,解得c.又a2=2+c2,即可得出$e=\frac{c}{a}$.
(2)曲线C的方程:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}$=1,F(1,0).设A(x1,y1),B(x2,y2),P(x,y).设直线l:x=ky+1(k≠0)代入椭圆方程可得:(2k2+3)y2+4ky-4=0,利用根与系数的关系及其$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,可得 P$(\frac{6}{2{k}^{2}+3},\frac{-4k}{2{k}^{2}+3})$,把P坐标代入椭圆方程,解得k,由于对称性知,当k=$\frac{\sqrt{2}}{2}$时,直线l:x-$\frac{\sqrt{2}}{2}$y-1=0,利用点到直线的距离公式可得:坐标原点到直线l的距离为d1,点P到直线l的距离为d2,|AB|.可得S=$\frac{1}{2}|AB|({d}_{1}+{d}_{2})$.
解答 解:(1)F(c,0),直线l的方程为:y=x-c,
可得:$\frac{c}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,解得c=1.
又a2=2+1=3,∴$e=\frac{c}{a}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
(2)曲线C的方程:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}$=1,F(1,0).
设A(x1,y1),B(x2,y2),P(x,y)
设直线l:x=ky+1(k≠0)代入椭圆方程可得:(2k2+3)y2+4ky-4=0,
∴y1+y2=$-\frac{4k}{2{k}^{2}+3}$,y1•y2=-$\frac{4}{2{k}^{2}+3}$.
x1+x2=k(y1+y2)+2=$\frac{6}{2{k}^{2}+3}$.
∵$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,
则 P$(\frac{6}{2{k}^{2}+3},\frac{-4k}{2{k}^{2}+3})$,
∵P在椭圆上,∴$2×\frac{36}{(2{k}^{2}+3)^{2}}$+3×$\frac{16{k}^{2}}{(2{k}^{2}+3)^{2}}$-6=0,
化为:4k4+4k2-3=0,解得k=$±\frac{\sqrt{2}}{2}$.
由于对称性知,当k=$\frac{\sqrt{2}}{2}$时,直线l:x-$\frac{\sqrt{2}}{2}$y-1=0,P$(\frac{3}{2},-\frac{\sqrt{2}}{2})$.
坐标原点到直线l的距离为d1=$\frac{\sqrt{6}}{3}$,点P到直线l的距离为d2=$\frac{\sqrt{6}}{3}$,
|AB|=$\sqrt{(1+2)[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\frac{3\sqrt{3}}{2}$.
∴S=$\frac{1}{2}|AB|({d}_{1}+{d}_{2})$=$\frac{3\sqrt{2}}{2}$.
点评 本题考查了直线与椭圆的相交弦长问题、点到直线的距离公式、向量坐标运算性质、三角形面积计算公式,考查了推理能力与计算能力,属于难题.


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 40 | C. | 35 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
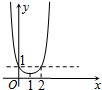
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
已知定义在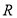 上的函数
上的函数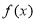 满足:
满足: 的图象关于
的图象关于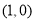 点对称,且当
点对称,且当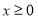 时恒有
时恒有 ,当
,当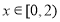 时,
时,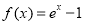 ,则
,则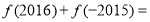 ( )
( )
A.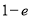 B.
B.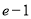
C.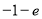 D.
D.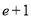
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com