
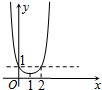
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (0,2) |
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:解答题
 如图,四棱锥B-ACDE的底面ACDE满足 DE∥AC,AC=2DE.
如图,四棱锥B-ACDE的底面ACDE满足 DE∥AC,AC=2DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 作文成绩优秀 | 作文成绩一般 | 合计 | |
| 阅读量大 | 18 | 9 | |
| 阅读量少 | 8 | 15 | |
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| y1 | y2 | 总计 | |
| x1 | * | 16 | 40 |
| x2 | a | b | * |
| 总计 | 28 | * | 70 |
| A. | 14,16 | B. | 4,26 | C. | 4,24 | D. | 26,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1 | B. | 0.01 | C. | 0.9 | D. | 0.99 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数 .
.
(1)若函数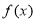 在
在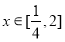 内单调递减,求实数
内单调递减,求实数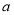 的取值范围;
的取值范围;
(2)当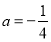 时,关于
时,关于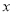 的方程
的方程 在
在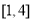 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数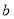 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com