
 如图,四棱锥B-ACDE的底面ACDE满足 DE∥AC,AC=2DE.
如图,四棱锥B-ACDE的底面ACDE满足 DE∥AC,AC=2DE.分析 用分析法证明第(Ⅰ)问,用反证法证明第 (Ⅱ)问,根据分析法、反证法的证明步骤,即可得出结论.
解答 (Ⅰ)证明:欲证平面ABE⊥平面BCD,
只需证AB⊥平面BCD,----------------------------------------------(2分)
由已知AB⊥BC,只需证AB⊥DC,-------------------------------------------------(4分)
由已知DC⊥平面ABC可得DC⊥AB成立,
所以平面ABE⊥平面BCD.
(Ⅱ)证明:假设在平面ABE内存在直线与DC平行,---------------------------------(6分)
又因为DC?平面ABE,所以DC∥平面ABE.
又因为平面ACDE∩平面ABE=AE,
所以DC∥AE,---------------------------------------(8分)
又因为DE∥AC,所以ACDE是平行四边形,
所以AC=DE,这与AC=2DE矛盾,---------------------------------------------(10分)
所以假设错误,原结论正确.
故答案为AB⊥平面BCD;AB⊥DC;在平面ABE内存在直线与DC平行;DC∥AE;AC=2DE.
点评 本题考查分析法、反证法,考查学生分析解决问题的能力,正确运用分析法、反证法是关键.


科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
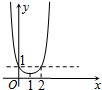
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com