
分析 (1)由抛物线的焦点坐标(0,1),求得a和b的关系,由C1与C2的公共点的坐标为(±$\sqrt{6}$,$\frac{3}{2}$),代入椭圆方程,即可求得a和b的值,求得椭圆方程;
(2)设直线l的方程为y=k(x+1),代入椭圆方程,利用韦达定理及向量数量积的坐标运算,即可求得$∠AOB>\frac{π}{2}$,可知O恒在为AB直径的圆内,故不存在实数k.
解答 解:(1)由C1:x2=4y知其焦点F的坐标为(0,1).
因为F也是椭圆C2的一个焦点,所以a2-b2=1.①
又C1与C2的公共弦的长为$2\sqrt{6}$,C1与C2都关于y轴对称,
且C1的方程为x2=4y,
由此易知C1与C2的公共点的坐标为(±$\sqrt{6}$,$\frac{3}{2}$),所以$\frac{9}{{4{a^2}}}+\frac{6}{b^2}=1$.②
联立①,②得a2=9,b2=8.
故C2的方程为$\frac{y^2}{9}+\frac{x^2}{8}=1$.
(2)由题意直线l的斜率存在,设直线l的方程为y=k(x+1),
联立方程$\left\{{\begin{array}{l}{8{y^2}+9{x^2}=72}\\{y=kx+k}\end{array}}\right.$,
整理得 (9+8k2)x2+16k2x+8k2-72=0.
设A(x1,kx1+k),B(x2,kx2+k),
于是有x1+x2=$\frac{{-16{k^2}}}{{9+8{k^2}}}$,x1x2=$\frac{{8{k^2}-72}}{{9+8{k^2}}}$.
因为$\overrightarrow{OA}=({{x_1},k{x_1}+k}),\overrightarrow{OB}=({{x_2},k{x_2}+k})$,
$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+(kx1+k)(kx2+k)=$({1+{k^2}}){x_1}{x_2}+{k^2}({{x_1}+{x_2}})+{k^2}$=$\frac{{-55{k^2}-72}}{{9+8{k^2}}}<0$.
所以$∠AOB>\frac{π}{2}$.
可知O恒在为AB直径的圆内.
∴不存在实数k,使O在以AB为直径的圆外.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
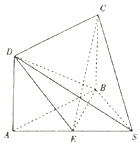 如图,在四棱锥S-ABCD中,四边形为ABCD矩形,E为SA的中点,SA=SB,AB=2$\sqrt{3}$,BC=3.
如图,在四棱锥S-ABCD中,四边形为ABCD矩形,E为SA的中点,SA=SB,AB=2$\sqrt{3}$,BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
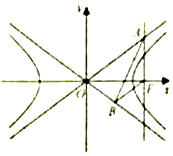 如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,6} | B. | {1,3,5} | C. | {1,3,5,7} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com