Question

【题目】

某投资公司在2010年年初准备将1000万元投资到“低碳”项目上，现有两个项目供选择：

项目一：新能源汽车．据市场调研，投资到该项目上，到年底可能获利，也可能亏损，且这两种情况发生的概率分别为和；

项目二：通信设备．据市场调研，投资到该项目上，到年底可能获利，可能亏损，也可能不赔不赚，且这三种情况发生的概率分别为、和

（Ⅰ）针对以上两个投资项目，请你为投资公司选择一个合理的项目，并说明理由；

（Ⅱ）若市场预期不变，该投资公司按照你选择的项目长期投资（每一年的利润和本金继续用作投资），问大约在哪一年的年底总资产（利润＋本金）可以翻一番？

（参考数据：，）

Answer 1

【答案】（Ⅰ）建议该投资公司选择项目一投资；（Ⅱ）大约4年后，即在2013年底总资产可以翻一番.

【解析】

（Ⅰ）根据两个项目获利的数学期望的大小可选择合理的项目.

（Ⅱ）假设年后总资产可以翻一番，则有，利用对数的运算及给出的数据可求大约4年后翻一番.

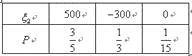
（1）若按“项目一”投资，设获利万元，则的分布列为：

（万元），

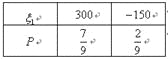
若按“项目二”投资，设获利万元，则的分布列为：

（万元），

又，

，

所以，，这说明虽然项目一、项目二获利相等，但项目一更稳妥．

综上所述，建议该投资公司选择项目一投资．

（2）假设年后总资产可以翻一番，依题意：，即，10分

两边取对数得：．

所以大约4年后，即在2013年底总资产可以翻一番．