
【题目】已知函数![]() ,g(x)=b(x﹣1),其中a≠0,b≠0
,g(x)=b(x﹣1),其中a≠0,b≠0
(1)若a=b,讨论F(x)=f(x)﹣g(x)的单调区间;
(2)已知函数f(x)的曲线与函数g(x)的曲线有两个交点,设两个交点的横坐标分别为x1,x2,证明:![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)求导得![]() ,按照a>0、 a<0讨论
,按照a>0、 a<0讨论![]() 的正负即可得解;
的正负即可得解;
(2)设x1>x2,转化条件得![]() ,令
,令![]() ,
,![]() ,只需证明
,只需证明![]() 即可得证.
即可得证.
(1)由已知得![]() ,
,
∴![]() ,
,
当0<x<1时,∵1﹣x2>0,﹣lnx>0,∴1﹣x2﹣lnx>0,;
当x>1时,∵1﹣x2<0,﹣lnx<0,∴1﹣x2﹣lnx<0.
故若a>0,F(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
故若a<0,F(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
(2)不妨设x1>x2,依题意![]() ,
,
∴![]() ,同理得
,同理得![]()
由①﹣②得,∴![]() ,
,
∴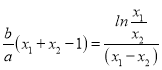 ,
,
∴![]() ,
,
故只需证![]() ,
,
取∴![]() ,即只需证明
,即只需证明![]() ,
,![]() 成立,
成立,
即只需证![]() ,
,![]() 成立,
成立,
∵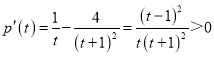 ,
,
∴p(t)在区间[1,+∞)上单调递增,
∴p(t)>p(1)=0,t>1成立,
故原命题得证.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】
某投资公司在2010年年初准备将1000万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利![]() ,也可能亏损
,也可能亏损![]() ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利![]() ,可能亏损
,可能亏损![]() ,也可能不赔不赚,且这三种情况发生的概率分别为
,也可能不赔不赚,且这三种情况发生的概率分别为![]() 、
、![]() 和
和![]()
(Ⅰ)针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由;
(Ⅱ)若市场预期不变,该投资公司按照你选择的项目长期投资(每一年的利润和本金继续用作投资),问大约在哪一年的年底总资产(利润+本金)可以翻一番?
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为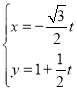 ,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2
,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2![]() sinθ,
sinθ,
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)直线l与x轴交于点P,与曲线C交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如图,已知椭圆E:
中,如图,已知椭圆E:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() .设直线
.设直线![]() 倾斜角的余弦值为
倾斜角的余弦值为![]() ,圆
,圆![]() 与以线段
与以线段![]() 为直径的圆关于直线
为直径的圆关于直线![]() 对称.
对称.
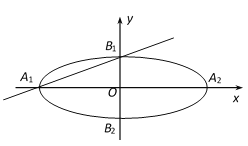
(1)求椭圆E的离心率;
(2)判断直线![]() 与圆
与圆![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆![]() 的面积为
的面积为![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理“幂势既同,则积不容异”中的“幂”指面积,“势”即是高,意思是:若两个等高的几何体在所有等高处的水平截面的面积恒等,则这两几何体的体积相等.设夹在两个平行平面之间的几何体的体积分别为![]() ,它们被平行于这两个平面的任意平面截得的两个截面面积分别为
,它们被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 恒成立”是“
恒成立”是“![]() ”的( )
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设θ∈[0,π],且f(θ)![]() 1,求θ的值;
1,求θ的值;
(2)在△ABC中,AB=1,f(C)![]() 1,且△ABC的面积为
1,且△ABC的面积为![]() ,求sinA+sinB的值.
,求sinA+sinB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com