
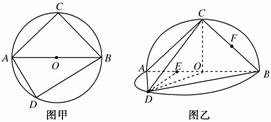
如图甲,⊙O的直径AB=2,圆上两点C、D在直径AB的两侧,且∠CAB= ,∠DAB=
,∠DAB=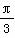 .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
(1)求三棱锥C-BOD的体积;
(2)求证:CB⊥DE;
(3)在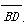 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
解析: (1)∵C为圆周上一点,且AB为直径,∴∠C=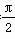 ,
,
∵∠CAB=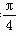 ,∴AC=BC,
,∴AC=BC,
∵O为AB的中点,∴CO⊥AB,
∵AB=2,∴CO=1.
∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,
∴CO⊥平面ABD,∴CO⊥平面BOD.
∴CO就是点C到平面BOD的距离,
S△BOD=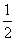 S△ABD=
S△ABD=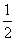 ×
×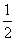 ×1×
×1×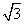 =
=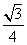 ,
,
∴VC-BOD=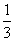 S△BOD·CO=
S△BOD·CO=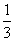 ×
×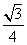 ×1=
×1=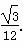 .
.
(2)证明:在△AOD中,∵∠OAD=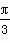 ,OA=OD,
,OA=OD,
∴△AOD为正三角形,
又∵E为OA的中点,∴DE⊥AO,
∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,
∴DE⊥平面ABC.
又CB⊂平面ABC,∴CB⊥DE.
(3)存在满足题意的点G,G为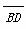 的中点.证明如下:
的中点.证明如下:
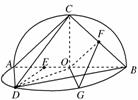
连接OG,OF,FG,
易知OG⊥BD,
∵AB为⊙O的直径,
∴AD⊥BD,
∴OG∥AD,
∵OG⊄平面ACD,AD⊂平面ACD,
∴OG∥平面ACD.
在△ABC中,O,F分别为AB,BC的中点,
∴OF∥AC,
∴OF∥平面ACD,
∵OG∩OF=O,
∴平面OFG∥平面ACD.
又FG⊂平面OFG,∴FG∥平面ACD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
设P和Q是两个集合,定义集合P-Q={x|x∈P,且xQ},如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆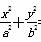 =1(a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
=1(a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
A.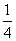 B.
B.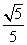
C. D.
D.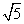 -2
-2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知正项数列{an},其前n项和Sn满足6Sn=a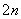 +3an+2,且a1,a2,a6是等比数列{bn}的前三项.
+3an+2,且a1,a2,a6是等比数列{bn}的前三项.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=a1bn+a2bn-1+…+anb1,n∈N*,证明:3Tn+1=2bn+1-an+1(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的有( )
A.若m∥α,n∥α,则m∥n B.若α⊥γ,β⊥γ,则α∥β
C.若m∥α,m∥β,则α∥β D.若m⊥α,n⊥α,则m∥n
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,点C是以AB为直径的圆上的一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=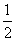 BC.
BC.
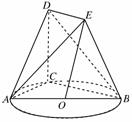
(1)证明:EO∥平面ACD;
(2)证明:平面ACD⊥平面BCDE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com