
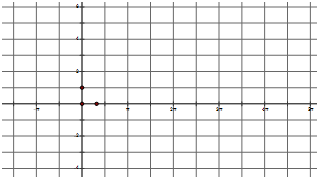
分析 (1)由已知求出周期,进一步求得ω,再由函数为偶函数求得φ,则函数解析式可求;
(2)通过函数的图象平移求得函数g(x)的解析式,并求出函数的对称中心,然后利用五点作图作出函数的图象.
解答 解:(1)∵函数y=f(x)图象的两相邻对称轴间的距离为$\frac{π}{2}$,∴周期T=π.
则ω=$\frac{2π}{T}=\frac{2π}{π}=2$,函数f(x)=2sin(2x+φ),
又函数f(x)=2sin(2x+φ)(0<φ<π)为偶函数,
则2sinφ=2,即sinφ=1,∴φ=$\frac{π}{2}$.
∴f(x)=2sin(2x+$\frac{π}{2}$)=2cos2x;
(2)将函数y=f(x)的图象向右平移$\frac{π}{3}$个单位后,所得函数解析式为y=2cos2(x-$\frac{π}{3}$)=2cos(2x-$\frac{2π}{3}$),
再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,解析式为g(x)=$2cos(\frac{1}{2}x-\frac{2π}{3})$.
由$\frac{1}{2}x-\frac{2π}{3}=\frac{π}{2}+kπ$,得x=$\frac{7π}{3}+2kπ$,k∈Z.
∴函数g(x)的对称中心为($\frac{7π}{3}+2kπ$,0),k∈Z;
列表:
| x | 0 | $\frac{4π}{3}$ | $\frac{7π}{3}$ | $\frac{10π}{3}$ | 4π | $\frac{13π}{3}$ |
| $\frac{1}{2}x-\frac{2π}{3}$ | $-\frac{2π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{4π}{3}$ | $\frac{3π}{2}$ |
| y | -1 | 2 | 0 | -2 | -1 | 0 |
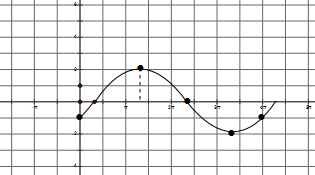
点评 本题考查三角函数的图象平移,考查了y=Asin(ωx+φ)型函数的图象及性质,是中档题.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $log_2{\frac{15}{2}}$ | C. | 1 | D. | $-log_2{\frac{15}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,AB⊥AD,AB=3,CD=2,PD=AD=5.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,AB⊥AD,AB=3,CD=2,PD=AD=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
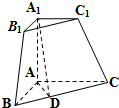 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=$\sqrt{2}$,AC=2,A1C1=1,$\frac{BD}{DC}$=$\frac{1}{2}$.
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=$\sqrt{2}$,AC=2,A1C1=1,$\frac{BD}{DC}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0).且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,x≥0}\\{-\frac{1}{2}x+1,x<0}\end{array}\right.$的图象上.若在矩形ABCD内随机取一点,则该点取自空白部分的概率等于( )
如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0).且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,x≥0}\\{-\frac{1}{2}x+1,x<0}\end{array}\right.$的图象上.若在矩形ABCD内随机取一点,则该点取自空白部分的概率等于( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,2) | C. | (0,2) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com